Archive 2017-2018

Comité local d’organisation

SPOT 54. Lundi 28 mai 2018. Lieu : N7, salle des thèses

14h – Nick Trefethen (Univ of Oxford and ENS Lyon)  – Axis-alignment in Low Rank and Other Structures

In two or more dimensions, various methods have been developed to represent matrices or functions more compactly. The efficacy of such methods often depends on alignment of the data with the axes. We shall discuss four cases: low-rank approximations, quasi-Monte Carlo, sparse grids, and multivariate polynomials.

15h – Simon Foucart (Texas A&M Univ)  – Semidefinite Programming in Approximation Theory: Two Examples

This talk aims at advocating interplays between Optimization and Approximation Theory by describing two successful examples. In the first example, we exploit a semidefinite characterization for the nonnegativity of univariate polynomials to devise a method for computing best approximants by splines under constraints. This is implemented as a MATLAB package called Basc. In the second example, we leverage the method of moments to tackle the long-standing problem of minimal projections. In particular, we determine numerically the projection constants for the spaces of cubic, quartic, and quintic univariate polynomials.

 

SPOT 53. lundi 16 avril 2018. Lieu : N7, salle A202.

14h – Emilio Carrizosa (Instituto de Matemáticas de la Universidad de Sevilla) – Mathematical optimization problems in cost-sensitive classification

Two benchmark procedures in Data Science, namely, Support Vector Machines (SVM) and Classification and Regression Trees (CART), have difficulties to properly address problems in which misclassification costs are unbalanced. In this talk we will discuss cost-sensitive variants of SVM and CART, expressed as (Mixed Integer) Mathematical Optimization problems. The numerical experience reported shows the practical pertinence of our approach(es).

15h – Frédéric de Gournay (IMT – INSA de Toulouse) – A representation theorem of sparse solutions by convex regularization

This talk will show-case a recent representation theorem for convex regularisation. In a nutshell, with very few hypothesis, it is shown that if one has m measurements and regularises a possibly non-convex data-fitting term with a norm then there exists a solution which is a positive combination of at most m extreme points of the norm. If the data-fitting term is convex it is possible to characterise the set of solutions. Several extensions are proposed especially when the regularizing term is not supposed to be a norm. The theorem holds in infinite dimension allowing for example to caracterize the convex regularisation by the TV semi-norm.

Joint work with Vincent Duval INRIA (France), Pierre Weiss ITAV (France), Claire Boyer LPSM (France), Antonin Chambolle CMAP (France), Yohann De Castro Orsay (France)

SPOT 52. Lundi 19 mars 2018. Lieu : N7, salle des thèses.

14h – Dominique Orban (GERAD, Montréal). A Regularized Factorization-Free Method for Equality-Constrained Optimization

We propose a factorization-free method for equality-constrained optimization based on a problem in which all constraints are systematically regularized. The regularization is equivalent to applying an augmented Lagrangian method but the linear system used to compute a search direction is reminiscent of regularized sequential quadratic programming (SQP). A limited-memory BFGS approximation to second derivatives allows us to employ iterative methods for linear least squares to compute steps, resulting in a factorization-free implementation. We establish global and fast local convergence under weak assumptions.
In particular, we do not require the LICQ and our method is suitable for degenerate problems. Numerical experiments show that our method significantly outperforms IPOPT with limited-memory BFGS approximations. We include a discussion on generalizing our framework to other classes of methods and to problems with inequality constraints.

15h – Justin Carpentier (LAAS-CNRS, Toulouse) – Optimization in Robotics

This talk deals with the problem of locomotion of robotic systems, and mostly of humanoid robots.

I will first introduce the basic concepts of locomotion and I will show how the problem of humanoid locomotion can be formulated as a big and complex optimal control problem. I will then show how we can cut this optimal control problem into smaller optimal control problems, simpler to solve by exploiting the geometric properties of the locomotion problem itself. Finally, I will introduce some personal perspectives on how to tackle the curse of dimensionality which is inherent to robotics.

All along this presentation, I will present the optimization tools that we use and we are currently developing in robotics in order to solve the locomotion, within the scope of real-time motion generation.

SPOT 51. lundi 12 février 2018. Lieu : Salle des thèses N7.

14h – Francisco Silva (XLIM) : Finite mean field games: fictitious play and convergence analysis.

 In this talk, based on an ongoing work with S. Hadikhanloo (U. Paris-Dauphine), we consider a class of finite state and discrete time Mean Field Games (MFGs) introduced by Gomes, Mohr and Rigao Souza in 2009. In this framework we first study an adaptation of the fictitious play procedure for continuous MFGs, introduced recently by Cardaliaguet and Hadikhanloo, and we prove the convergence to the solution of the finite MFG. In the second part of the talk, we consider a first order continuous MFG and an associated family of finite MFGs, parameterized by a finite time and space grid. We prove that, as the time and space steps tend to 0, the solutions of the finite MFGs converge to a solution of the continuous one.

15h – Jérôme Bertrand (IMT UPS, Toulouse) : Kantorovitch rencontre Alexandrov.

Dans cet exposé, je présenterai une version non-linéaire d’un problème introduit dans les années 40 par Kantorovitch pour étudier le problème de transport optimal de masse. Ce problème non-linéaire consiste à maximiser une fonctionnelle « DC » sous une contrainte convexe non-compacte (la même que dans le problème initial). La motivation principale pour étudier ce problème est son utilisation pour résoudre un problème de prescription de la courbure des ensembles convexes. Ce problème, initialement introduit par Alexandrov dans ces mêmes années 40, peut se démontrer, dans l’espace euclidien, à l’aide d’une forme adéquate de la fonctionnelle de Kantorovitch. Le problème non-linéaire que je présenterai permet de résoudre l’analogue du problème d’Alexandrov pour les convexes de l’espace hyperbolique.

Cet exposé sera principalement consacré au problème d’optimisation et ne nécessitera aucune connaissance préalable en géométrie hyperbolique. Il est basé sur un travail en collaboration avec Philippe Castillon.

 

SPOT 50. lundi 29 janvier 2018. Lieu : Salle des thèses N7.

14h – Marc Teboulle (Scool of mathematical Sciences, Tel Aviv University)

Another Look at First Order Methods: Lifting the Lipschitz Gradient Continuity Restriction

The gradient method, invented by Cauchy about 170 years ago, is today an icon in modern optimization algorithms and applications, through many of its relatives/variants class of First order methods (FOM). They have attracted over the last decade intensive research activities, and are still conducted at a furious path. This is due to their computational simplicity and adequacy
for solving to medium accuracy, very large scale  structured optimization problems which naturally arise in a huge spectrum of scientific applications.

A crucial and standard  assumption common to almost all  (FOM)  requires the gradient of the smooth part in a given objective function to be globally Lipschitz continuous,  precluding the use of FOM in many important applied scenarios.

In this talk, we introduce a simple and elegant framework for FOM, which allows to circumvent this longstanding smoothness restriction by capturing all at once, the geometry of the objective and the feasible set.  The new framework translates  into first order methods with proven guaranteed complexity estimates, and pointwise global convergence for the fundamental composite convex optimization model. It paves a new path for tackling broad classes of problems, which were until now considered  as out of reach via first order schemes. This will be illustrated through the derivation of new and simple schemes for Poisson linear inverse problems.

Joint work with H. Bauschke (UBC) and J. Bolte (TSE).

15h – Shoham Sabach (Technion Haifa)

First Order Methods for Solving Convex Bi-Level Optimization Problems

We study convex bi-level optimization problems for which the inner level consists of minimization of the sum of smooth and nonsmooth functions. The outer level aims at minimizing a smooth and strongly convex function over the optimal
solutions set of the inner problem. We analyze first order methodsand global sublinear rate of convergence of the method is established in terms of the inner objective function values.

The talk is based on joint work with Shimrit Shtern (Technion).

SPOT 49. lundi 11 décembre 2017. Lieu : salle des thèses N7.

14h – Miguel Angel Goberna (Univ. Alicante)

Farkas’ lemma: some extensions and applications

The classical Farkas’ lemma characterizing the linear inequalities which are consequence of an ordinary linear system was proved in 1902 by this Hungarian Physicist to justify the first order necessary optimality condition for nonlinear programming problems stated by Ostrogradski in 1838. At present, any result characterizing the containment of the solution set of a given system in the sub-level sets of a given function is said to be a Farkas-type lemma. These results provide partial answers to the so-called containment problem, consisting in characterizing the inclusion of a given set into another one. In this talk we provide different Farkas-type lemmas, in finite and infinite dimensional spaces, involving scalar and vector functions. We also discuss their applications in semi-infinite and infinite optimization.

15h – Alfred Galichon (New York University, FAS and Courant Institute)

Vector Quantile Regression: an overview and some open problems

Vector Quantile Regression was introduced in a recent paper by Carlier, Chernozhukov and myself as a way to provide a parametric representation of the conditional distribution of a random dependent vector given a vector of covariates, in the spirit of Brenier’s theorem in the theory of optimal transport. After recalling the basic results (which constitute an extension of Monge-Kantorovich duality) and their applications to econometrics and biometrics, I will describe some open computational and theoretical problems.

SPOT 48. Jeudi 16 novembre 2017. Lieu : salle des thèses N7.

14h – Bernard Dacorogna (EPFL Lausanne)

Théorème de Darboux, factorisation symplectique et ellipticité
Notre premier résultat concerne le théorème classique de Darboux. On montre que si ω_m est la forme symplectique standard dans R^{2m} et f est une forme symplectique quelconque, alors on peut trouver un difféomorphisme φ, avec régularité optimale, satisfaisant:

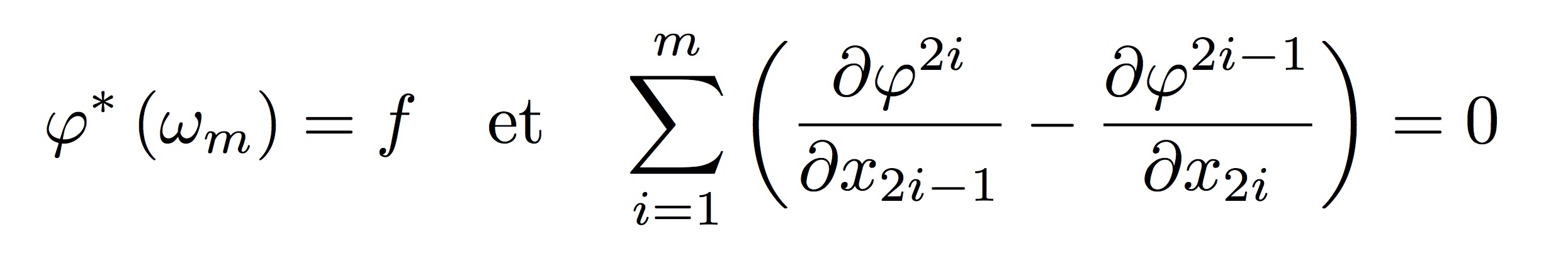
dacorogna_1
pour autant que f soit proche de ω_m. De plus le système ci-dessus est elliptique et nous avons unicité si l’on prescrit une condition de Dirichlet sur le bord.On applique alors ce résultat à ce que nous appelons la factorisation symplectique. Nous montrons que n’importe quelle application  satisfaisant des hypothèses appropriées, peut-être écrite comme:

φ = ψ o χ

où

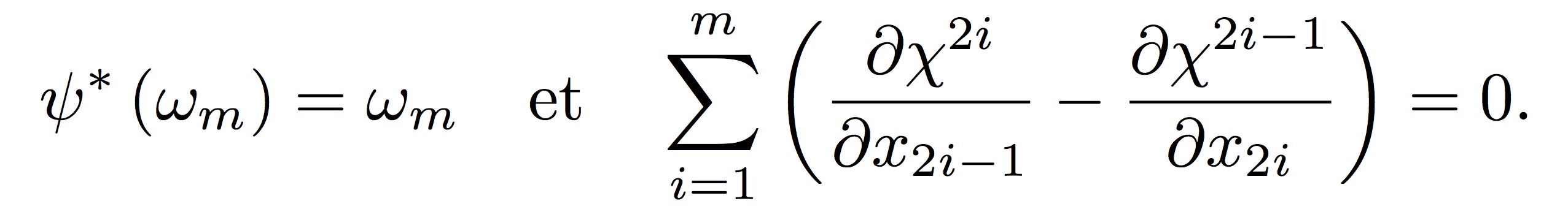dacorogna_2L’analogie avec le cas des formes volumes sera discutée longuement. Le premier système devient alors l’équation de Monge Ampère; alors que (2) n’est rien d’autre que la factorisation polaire classique. Ce travail a été effectué en collaboration avec W. Gangbo et O. Kneuss.

15h – Pierre Bousquet (IMT Toulouse)
Un problème variationnel dégénéré
Nous présentons un problème scalaire multidimensionnel en calcul des variations avec un intégrande convexe qui n’est ni régulier, ni strictement convexe. Nous décrivons la régularité des solutions et analysons le problème d’unicité des solutions. Il s’agit d’un travail en collaboration avec Guy Bouchitté.

 

SPOT 47. Lundi 9 octobre 2017. Lieu : A202 à l’N7.

14h - Térence Bayen (Univ. Montpellier) – Minimisation du temps de crise et applications

Dans cet exposé, on s’intéresse à la minimisation de la fonctionnelle dite « temps de crise » et qui représente le temps passé par une solution d’un système dynamique contrôlé à l’extérieur d’un ensemble donné. Cet ensemble représente des contraintes d’état ; pour des systèmes biologiques par exemple, il peut s’agir de contraintes écologiques. Minimiser le temps de crise permet donc de trouver une trajectoire qui reste le moins longtemps possible en dehors de ces contraintes. La fonction temps de crise possède la particularité d’être discontinue et on s’intéressera d’abord aux conditions d’optimalité du premier ordre (type Pontryagin) afin de synthétiser des lois de commande optimales. Pour ce faire, nous utiliserons le principe du maximum hybride. On étudiera également une régularisation de ce problème ainsi que la convergence des solutions du problème régularisé vers une solution du problème original par Gamma-convergence). Enfin, nous présenterons plusieurs exemples de calcul de stratégies optimales pour le temps de crise et notamment dans le cas du système Lotka-Volterra avec contrôle. Il s’avère alors que la minimisation du temps de crise offre une alternative originale à la stratégie de temps minimal pour rejoindre le noyau de viabilité.

15h - Jean-Luc Bouchot  (RWTH Aachen Univ) – Parametric function approximation in Hilbert spaces (and some applications to Galerkin approximations to high dimensional parametric elliptic PDEs)

I introduce ideas stemming from sparse approximation in signal processing (compressed sensing) and extend them to the context of function approximation. In particular, I consider the problem of approximating a Hilbert valued-function parametrized by a (potentially infinite but countable) sequence of coefficients. Our approximation is obtained by means of a weighted l1 minimization which generates sparse polynomial chaos expansions. As an application, I analyze the problem when the sought after function is solution to a parametric PDE which satisfies a stronger version of uniform ellipticity. We show that our approximation scheme is reliable and efficient, as it computes a uniform (with respect to the parameters) approximation in a computational time comparable to a single solve, hereby breaking the curse of dimensionality. This work is in collaboration with Holger Rauhut (RWTH Aachen) and Christoph Schwab (ETH Zurich).

 

SPOT 46. Lundi 25 septembre 2017. Lieu : A202 à l’N7.

14h – Etienne de Klerk (Univ Tilburg)

On the worst-case performance of the optimization methods of Cauchy and Newton for smooth strongly convex functions

We consider the Cauchy (or steepest descent) method with exact line search applied to a strongly convex function with Lipschitz continuous gradient. We establish the exact worst-case rate of convergence of this scheme, and show that this worst-case behavior is exhibited by a certain convex quadratic function. We also give a worst-case complexity bound for a noisy variant of the gradient descent method. Finally, we show that these results may be applied to study the worst-case performance of Newton’s method or the minimization of self-concordant functions. The proofs are computer-assisted, and rely on the resolution of semidefinite programming performance estimation problems as introduced in the paper [Y. Drori and M. Teboulle. Performance of first-order methods for smooth convex minimization: a novel approach. Mathematical Programming, 145(1-2):451-482, 2014]. This is joint work with F. Glineur and A.B. Taylor.

15h – Lieven Vandenberghe (Univ California Los Angeles)

Douglas-Rachford splitting and primal-dual first order methods
The primal-dual hybrid gradient method (or Chambolle-Pock method) is a popular first order method for large-scale convex optimization, particularly for nondifferentiable problems that arise in image processing and machine learning.  The method is known to include as a special case the Douglas-Rachford splitting algorithm for minimizing the sum of two convex functions. We show how, conversely, the primal-dual hybrid gradient algorithm can be derived from the Douglas-Rachford splitting algorithm. We also discuss implications for convergence analysis and related primal-dual algorithms.  (Joint work with Daniel O’Connor.)