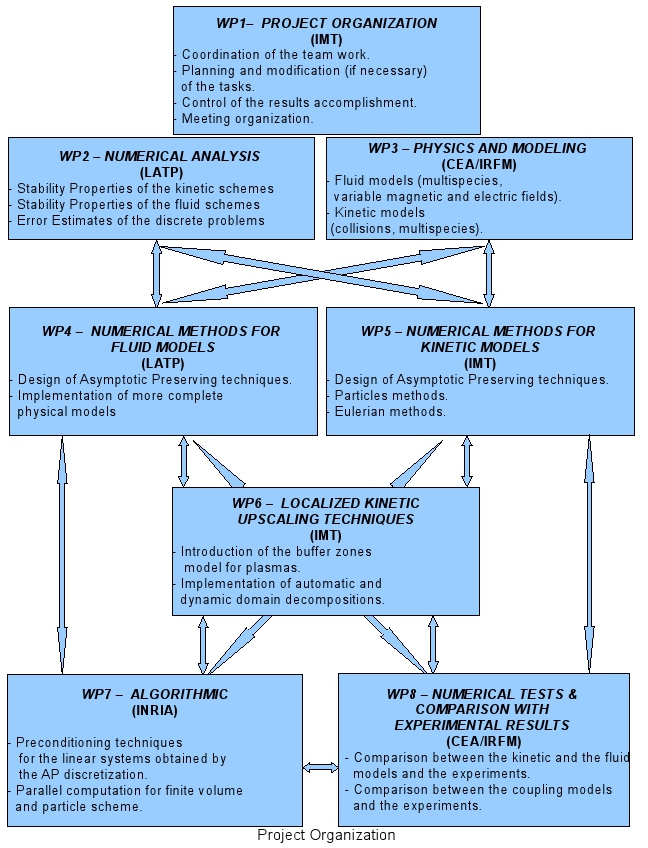
Scientific Program
Originality and novelty of the project
Fluid models: We will work on the development of numerical schemes for the Euler equations for charged particles subject to the Lorentz force. When the magnetic field is large, or equivalently, when the ion cyclotron frequency tends to zero, the so-called gyro-fluid approximation is obtained. In this limit, the parallel motion relative to the magnetic field direction splits from perpendicular motion and is given implicitly by the constraint of zero total force along the magnetic field lines. This equilibrium is attained through acoustic waves propagating at infinite velocity in a similar fashion as what happens in a low Mach number fluid. First goal of this project will be to work on the construction of Asymptotic-Preserving (AP) schemes for this problem.
Kinetic Models: A fluid description usually overestimates turbulent fluxes especially in a weakly collisional regime which is sometimes encountered in Tokamaks devices. In this case, the kinetic model provides an appropriate description of turbulent transport in a fairly general context, but it requires to solve a huge computational cost model. We aim to construct numerical schemes which in the limit will solve an asymptotic model obtained under both assumptions of large magnetic fields and low-Mach numbers. In several practical situations, collisions play an important role in order to obtain a correct physical description of the problem. To this aim, we will also consider the addition of the Landau-Fokker-Planck operator to the kinetic model and we will introduce appropriate numerical techniques to discretize it. Another aspect of the project will consists in combining the two approaches (kinetic and fluid) through the use of localized kinetic upscaling techniques.
Numerical Analysis of the methods: This part of the project is concerned with the numerical analysis of the methods we will develop. In details the idea is to work on the consistency and stability results for kinetic and fluid asymptotic preserving methods. Error estimates in terms of the mesh size and time step will be also searched. Our scope is to provide the necessary mathematical basis for the development of the methods.
Algorithm definition and implementation: A fundamental step in our project will be to establish open source software libraries for the simulation of plasmas that can be described by kinetic or fluid equations. For the fluid models we propose to develop a full 3-D solver for the asymptotic preserving gyro-fluid model. For the kinetic model we will be interested in the development of asymptotic preserving Monte Carlo-Particle in Cell solvers in the full three-dimensional case.
Work plan
Seven different tasks have been identified. An additional task the global organization will consist in supervising and coordinating the single tasks.
Numerical Analysis: When a new numerical method is developed limits and performances are not known. Thus, simple numerical tests are done in order to prove capability of the schemes of solving more complex problems. Although the numerical tests step is necessary, however an analysis of the mathematical properties of the schemes is also indispensable to fully master the techniques we intend to use. This task will provide the solution to these aspects. The responsible of the coordination will be the LATP Marseille.
Physics and Modeling: Numerical schemes which solve the simplified Euler equations for plasma simulations have already been considered. The scope of this project is the development of Asymptotic Preserving schemes for a large class of models describing magnetically confined plasmas. From the kinetic side we want to consider the case of different species and the coupling between the resulting kinetic equations. A very important aspect will be to consider the addition of the Landau-Fokker-Planck collision operator. The responsible of the coordination will be the CEA.
Numerical methods for fluid models: The gyro-fluid models are obtained by applying the drift approximation to the basic fluid-dynamic equations. However, this is a singular limit and the resulting model involves many different terms which make numerical approximations delicate. We propose, in this project, to investigate an alternate route, which consists in using the original equations of fluid dynamics without passing to the drift-approximation limit. These are schemes for the original fluid-dynamics model which allow the drift limit to be taken within the discrete approximation. The responsible of the coordination will be the LATP Marseille.
Numerical methods for kinetic models: we intend to construct AP schemes for the original Vlasov equation which in the limit will lead to a model of both large magnetic fields and low-Mach numbers. We will also work on the construction of such schemes in the case in which collisions will not be negligible. The responsible of the coordination will be the IMT of Toulouse.
Localized kinetic upscaling techniques: When a net distinction can be done between different regimes which can be described by different models we will provide a scheme which will be able to locally benefit of kinetic effects. From one side we will work on the definition of a breakdown criteria for the fluid models and to the other side we will introduce a coupling technique which has been already used in the case of rarefied gas dynamics. The resulting solver will be more efficient and will not lose in precision in the description of the solution compared to a full kinetic one. The responsible of the coordination will be the IMT of Toulouse.
High performance computing: We will provide the efficient implementation on modern massively parallel computing platforms of the asymptotic preserving scheme we will develop for the kinetic and the fluid models. In addition we will supervise their integration in application software in order to perform large-scale numerical simulations currently out of reach. The responsible of the coordination will be the INRIA team.
Numerical tests & comparisons: The first step will be a campaign of preliminary two dimensional tests which will be done for measuring the capability of the numerical schemes in reproducing known analytical solutions or classical tests cases. The second step will be the comparison with experimental results. The initial focus will be on evaluating the capability of the models to reproduce empirical scaling laws of plasma confinement. Detailed comparisons with specific measurements will be considered at the end of the project. The responsible of the coordination will be the CEA.