MISE A JOUR : LE PROGRAMME, LA LISTE DES PARTICIPANTS ET LE LIVRET DES RÉSUMÉS SONT DISPONIBLES.

Cette école est organisée par l’Institut de Mathématiques de Toulouse (UMR 5219) et le laboratoire SPHERE (UMR 7219). Elle est soutenue également par l’INSMI et l’INSHS du CNRS,  l’Université de Toulouse Paul Sabatier et la FREMIT,  l’Université Paris Diderot et son Département d’Histoire et Philosophie des Sciences, l’Institut Universitaire de France, la MSH de Clermont-Ferrand, l’IREPH (EA 373) et l’Ecole Doctorale « Connaissance, Langage, Modélisation » (ED 139), le CIRPHLES (USR 3308). Elle s’adresse prioritairement aux étudiants et jeunes chercheurs (Master M2, doctorants, post-doctorants), mathématiciens et philosophes.

Objectifs

Cette école thématique a pour but de développer la discussion et la collaboration entre mathématiciens et philosophes des mathématiques en confrontant les problématiques émergeant des pratiques mathématiques à l’œuvre dans les recherches contemporaines (par exemple, en géométrie algébrique ou en combinatoire) à celles issues du champ philosophique actuel (par exemple, la philosophie de la pratique mathématique).

Il s’agit à la fois de mettre les grandes questions philosophiques classiques (objectivité, unité, …) à l’épreuve des mathématiques contemporaines mais aussi, réciproquement, de susciter de nouvelles pistes en philosophie des mathématiques pouvant rendre compte d’un certain nombre de spécificités et de questions portées par les mathématiques contemporaines.

COURS

L’école thématique « Mathématiques et Philosophie Contemporaines » est organisée principalement suivant l’axe de « cours à quatre mains », dont sont à chaque fois co-responsables un mathématicien et un philosophe des mathématiques.

Le projet de ces cours est à la fois de donner un aperçu de différentes théories mathématiques, de présenter différentes problématiques philosophiques liées à ces théories et de promouvoir des collaborations effectives entre mathématiciens et philosophes. La participation aux cours supposera une familiarité minimale avec le contenu mathématique de ces cours.

L’un des enjeux de l’école thématique est de trouver la bonne distance en philosophie des mathématiques entre enjeux philosophiques et technicité mathématique, entre une tradition analytique qui privilégie la logique et des questions très générales à propos de l’objectivité mathématique, et une tradition continentale qui cherche à restituer les théories mathématiques dans leur détail technique.

Du côté des mathématiques, la prise en charge par les mathématiques elles-mêmes du statut des objets mathématiques qui sont introduits dans le cadre d’une théorie, fait que la réflexion sur le cadre ou les concepts fondamentaux d’une théorie est en prise directe avec un travail proprement mathématique. L’école thématique cherchera à donner des exemples précis de cette interaction.

Les conférenciers qui donneront les cours sont :

Philosophie

Andrew Arana, Purity of methods in contemporary mathematics.
Sébastien Gandon, Rota et les fondements de la combinatoire.
Brice Halimi, Théorie algébrique des ensembles.
Sébastien Maronne et David Rabouin, Style et théorie de la référence en mathématiques.

Mathématiques

Denis-Charles Cisinski , titre à préciser.
Etienne Fieux, Combinatoire et topologie.
Frédéric Patras, Y-a-t-il des structures combinatoires ?
Timothy Porter, Where do spaces come from ?
Michel Vaquié, Notions d’espace et de point en géométrie algébrique.

Livret des résumés des cours

Pré-requis

Les pré-requis en mathématiques et en philosophie sont de niveau Licence-Master. Afin de permettre la mise à niveau des participants, si nécessaire, des indications de lecture seront données pour chaque cours dans une bibliographie en fin de résumé. Des séances de préparation de l’école thématique seront organisées à Paris au  séminaire « Mathématiques et Philosophie : 19ème et 20ème siècle » et à Toulouse au Groupe de Travail de Philosophie des Mathématiques.

Programme

Les cours ont lieu le matin de 9h à 12h (Mathématiques) et l’après-midi de 16h à 19h (Philosophie) à la Maison des Planchettes.

Le mercredi après-midi 27 juin est libre.

La plage de 12h à 16h est laissée à dessein libre afin de favoriser les discussions informelles sur les cours. En outre, les deux cours de mathématiques et philosophie de chaque journée seront articulés du point de vue de la thématique ou des problèmes abordés.

Programme détaillé

INSCRIPTIONS

Liste des participants

Candidature

Le nombre de participants est limité à 25. Les candidatures pour participer à l’Ecole Thématique sont acceptées après avis du Comité Scientifique de l’Ecole. Elles doivent être envoyées par courrier électronique à l’adresse MPhCstflour@math.univ-toulouse.fr en précisant le nom et l’adresse professionnelle, en indiquant « candidature » dans le sujet et en joignant un bref CV.

Droits d’inscription

Une fois la candidature acceptée, des droits d’inscription doivent être acquittés pour confirmer l’inscription. Lesdroits d’inscriptionincluent un forfait pour l’hébergement en pension complète des participants à la Maison des Planchettes. Ce forfait prend en compte la subvention apportée par l’organisation de l’Ecole Thématique pour l’hébergement des participants.

L’école « Mathématiques et Philosophie Contemporaines » est une école thématique CNRS organisée avec le concours de la Formation Permanente du CNRS (Délégation Midi-Pyrénées). Les personnels CNRS (ingénieurs, boursiers, chercheurs) sont exonérés de droits d’inscription et de frais de séjour. Leurs frais de transport seront pris en charge par leur délégation CNRS d’appartenance. Les autres organismes devront financer eux-mêmes leurs personnels.

Tarifs

Personnel CNRS : gratuit

Etudiants /jeunes chercheurs (Master M2, doctorants, post-doctorants) : 100 euros

Chercheurs/enseignants chercheurs : 200 euros

Le paiement des droits d’inscription (par bon de commande, chèque, virement, ou carte bancaire) doit être effectué auprès de Tamara  Azaiez-Bontemps en lui transmettant le document ci-joint complété par mail ou par fax (de préférence pour les paiements par carte bancaire).

Mail : tamara.azaiez@math.univ-toulouse.fr
Fax : +33 (0)5-61-55-75-99

Bourses (Mise à Jour)

Pour financer leur voyage, les participants peuvent solliciter une bourse d’un montant forfaitaire de 100 euros par voyage auprès de l’organisation de l’Ecole Thématique (le préciser dans la candidature). Ces bourses sont en nombre limité et s’adressent prioritairement aux jeunes chercheurs (master, doctorants, post-doctorants).

Calendrier des opérations

15 mars 2012 : Ouverture des inscriptions
15 mai 2012 : Clôture des inscriptions
11 juin 2012 : Envoi des convocations

HEBERGEMENT

L’hébergement se fait en « chambre confort » (douche et toilettes dans la chambre) à la Maison des Planchettes (7 rue des Planchettes, 15100 Saint-Flour). Il est prévu du dimanche 24 juin avant le repas du soir au samedi 30 juin après le repas de midi.

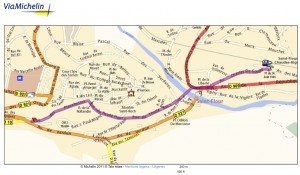
ACCÈS

En avion : Le plus proche aéroport est l’aéroport de Clermont-Ferrand Auvergne à Aulnat.

En train : Il existe six allers-retours par jour depuis Clermont-Ferrand avec un changement à Massiac-Blesle. Cf. la fiche horaire SNCF.

En voiture : Saint-Flour est située sur l’autoroute A75 à 100 km de Clermont-Ferrand (sorties 28 et 29).

Pour plus d’informations, consulter le site de l’Office de Tourisme de Saint-Flour.

COMITÉ D’ORGANISATION SCIENTIFIQUE

Denis-Charles Cisinski (Université Toulouse Paul Sabatier, IMT), Etienne Fieux (Université Toulouse Paul Sabatier, IMT), Sébastien Gandon (Université Clermont-Ferrand Blaise Pascal/IUF, PHIER), Brice Halimi (Université Paris Ouest Nanterre, IREPH), Sébastien Maronne (Université Toulouse Paul Sabatier, IMT), David Rabouin (CNRS, SPHERE), Joseph Tapia (Université Toulouse Paul Sabatier, IMT), Alexandre Teste (Délégation CNRS Midi-Pyrénées), Michel Vaquié (CNRS, IMT).

Contact : Pour tout contact, écrire à MPhCstflour@math.univ-toulouse.fr

LES TRANSPARENTS DES CONFERENCES SONT DISPONIBLES EN CLIQUANT SUR LES TITRES.

COLLOQUE FRANCO-RUSSE « LA LOGIQUE ET SES APPLICATIONS », 5-6 AVRIL 2012

Lieu du colloque : Université Paul Sabatier, Institut de Mathématiques de Toulouse, salle de conférence, Bât 1R3, 1^er étage.

Jeudi 5 avril, après-midi, session « Histoire de la logique »

14h15-15h45 Yury Chernoskutov (Université de Saint-Pétersbourg), Object  theory: its development in Austrian logic and philosophy of 19th century.

The attempt to trace the role of the object theory in the formation of modern logic is made in the report. The course of the object theory development in the framework of Austrian tradition of logic and philosophy is described, starting from its founder B.Bolzano. Implicit influence of Austrian objectual way of thinking via Brentano`s school on G.Frege (B.Kerry and K.Stumpf) and on B.Russell (A.Meinong) is enlighted. The connection of the object theory with the growth of non-classical applied logics is sketched.

16h-17h30 Olga Antonova (Saint-Pétersbourg, docteur en philosophie), Dedekind’s theory and development of logicism.

The fact that Dedekind’s conception of arithmetic influenced very much the development of mathematics in XX century is incontestable. Meanwhile nowadays there are many discussions about logical character of Dedekind’s conception of mathematics and in particular the relations between logicism in the sense of Frege and Dedekind’s mathematical theory. Can we say that Dedekind’s theory is a variant of traditional logicism? Is Dedekind logicist in the same sense as Frege? The aim of this talk is to examine logical aspects of Dedekind’s mathematical conception and analyze these aspects from the point of view of traditional logicism such as Frege’s theory. The study of the question about Dedekind’s logicism leads us to new comprehension of the rapport between set theory and symbolic logic in XIX- XX century. This problem is still unresolved and relevant to contemporary mathematics and logic.

Vendredi 6 avril, matin, session « Interaction de la logique avec un domaine formel »

9h30-11h Brice Halimi (Univ. Paris 10, SPHERE), Geometric Modal Logic.

Alethic modalities pertain to truths as being not only factual. The question as to whether a given proposition is possibly true is not answered by the fact that it is false (if it is false). The question as to whether a given proposition is necessarily true is not answered by the fact that it is true (if it is true). Modal questions, by their very nature, go beyond facts. Accordingly, modal logic should not be a factual science. Still, the range of what is possible (the content of the collection of all possible worlds, in modern modal semantics) is referred to as a kind of super-fact.

Modal logic should go beyond it: what the actual range of the possible turns out to be should be understood as a range among others. So apparently we are thrown back upon a new fact in the end, namely the range of all ranges for the possible. This is not so: the actual range of all possible ranges for the possible should itself be conceived of as a second-order range among others, within a third-order modal range.

In fact, it should not, but it may be conceived of in that way: everything depends on the level of modal iteration we are interested in. If we want to know whether a given proposition is possibly true (or necessarily true), we can be content with considering the actual range of all actual possible worlds. If we want to know whether the same proposition, supposed not to be possibly true, could have been possibly true, we should go beyond and consider the range of all possible first-order ranges of possible worlds. And so on and so forth.

I will argue that this intuition is at the core of modal reasoning and that the usual semantics for modal logic does not genuinely implement it. I will then suggest and set out an alternative semantical framework that interprets iterated modalities in a better way. In that framework, possible worlds of variable levels are introduced; for each modal iteration, a set of possible worlds is considered relatively to each already given possible world (the latter being thought of as the index of a modal level in discourse). The model of that picture will be the tangent space to a manifold, as devised in differential geometry.

11h15-12h45 Philippe Balbiani (CNRS, IRIT), Region-based theories of spaces

We will present formal languages interpreted over classes of structures featuring regions and relations between them. These languages stem from Whitehead’s system in which the “being in contact” relation was assumed as primitive and Grzegorczyk’s system in which the “being included” and “being separated” relations were assumed as primitives. We will provide a context for studying the confluence of four research areas: first-order mereotopologies, algebras of regions, region-based propositional modal logics of space and qualitative spatial reasoning.

Vendredi 6 avril, après-midi, session « Application de la logique à un domaine non formel »

14h15-15h45 Elena Lisanyuk (Université de Saint-Pétersbourg), How we do logic of norms in Russia: from 1958 up to now.

In my paper I am intended to suggest an overview of the development of logic of norms in Russia from three perspectives: theoretical, historical and sometimes from that of sociology of science. Projects dealing with inferential and semantic aspects of norms form the logical group which is the largest and is most respected in the Russian deontic horizon. Computation and normative reasoning make another research trend which focuses upon creating logical frameworks for legal data-bases and particular applications based on fuzzy and dynamic logic. Yet another direction is normative aspects in philosophy of law and ethics especially in what concerns the normative use of language in its analytical approach.

Deontic logic in the USSR and Russia enjoyed an exceptional fate. It started in the years of onrush of logic, flourished during the time of rapid development of its new branches (temporal, many-valued, action-oriented, non-monotonic, etc) and of yet newer semantic frameworks, survived in the considerable research decline in the years of reforms (1990-ies) and today went on creating various deontic applications in the field of philosophical logic, computer science and philosophy.

The beginning of deontic logic in Russia goes back to the year of 1958 when the first paper in Russian was published. Notwithstanding its rather young age, up to nowadays it has passed three periods:

(1) the rise and the first results (1958-1973), from the first paper to the first system;

(2) the systematic research and the foundation of a research community (1980-1990ies), from basic approaches to the development of non-standard systems (multi-modal (temporal), many-valued and dynamic);

(3) the development of non-monotonic and higher-order deontic systems and their legal applications (from 1990-ies up to the present day), from non-standard deontic systems to the their fuzzy applications in the legal data-bases.

16h-17h30 Yuri Nechitaylov (Saint-Petersburg State University), Epistemic Logic for bounded rationality.

A uniform semantic basis of the problem of logical omniscience is proposed. The basis stands on a comparison of Kripke semantics with complete and incomplete games. The ways to solve the problem by deviating the principle of compositionality of the possible worlds semantics is outlined. As a summary an Epistemic Logic for Bounded Rationality is sketched.

Organisation :

Olga Antonova (Saint-Pétersbourg, docteur en philosophie), olgaantonova73@gmail.com

Brice Halimi (Univ. Paris 10, SPHERE), bhalimi@u-paris10.fr

Sébastien Maronne (Univ. Toulouse Paul Sabatier, IMT), smaronne@math.univ-toulouse.fr

Avec le soutien de l’IMT, de la FREMIT et de l’IRIT.

MISE A JOUR : LES TRANSPARENTS DES EXPOSES SONT DISPONIBLES EN CLIQUANT SUR LES TITRES.

WORKSHOP « HOMOTOPIE », 20-21 octobre 2011

Lieu du workshop : Université Paul Sabatier, Institut de Mathématiques de Toulouse, salle de conférence, Bât 1R3,  1er étage.

Jeudi 20 octobre, après-midi, session Histoire

14h15-15h45 Renaud Chorlay (Univ. Paris 4, SPHERE), Homotopie : quelques repères historiques.

Nous proposons un exposé d’histoire récurrente, en présentant des textes qui, sur la période 1850-1930, contribuent à l’enrichissement conceptuel des notions homotopiques élémentaires de la topologie. Dans les années 1895-1905, la synthèse de Poincaré marque une étape fondamentale. On montrera en quoi elle noue ensemble des fils apparus en analyse (souvent complexe) dans des questions de natures différentes : intégrales curvilignes (ou d’ordres supérieurs) ; prolongement analytique ; étude de la multiformité de fonctions définies implicitement par des équations algébriques, des équations différentielles à coefficients algébriques, des équations analytiques. De 1850 à 1900, l’enrichissement conceptuel passe par la distinction progressive des contextes homologiques et homotopiques, par l’introduction de la notion de groupe, et par celle de revêtements remarquables (universel, d’orientation). Sur la période 1905-1930, nous suivrons deux fils : celui de la diffusion de la notion de revêtement au-delà de la théorie au sein duquel elle était apparue (la théorie de l’uniformisation), et celui des travaux de Brouwer puis Hopf sur les classes d’homotopie d’applications entre variétés compactes orientables.

16h-17h30 Ralf Krömer (Univ. Siegen), Groupe/groupoïde fondamental: le définir, établir ses propriétés, l’utiliser 1920-1960.

On présentera une histoire partielle des développements autour du concept de groupe fondamental dans la période indiquée, en comparant les diverses contributions par rapport aux questions suivantes: comment et sur quel ensemble/quels objets définit-on la composition, s’agit-il d’une loi de composition totale ou partielle, comment prouve-t-on les propriétés de base, quels sont les usages qu’on en fait, comment tout cela est-il encastré dans une théorie, un arsenal de méthodes etc. Parmi les multiples généralisations qu’a subi le concept (groupes d’homotopie etc.), on s’intéressera plus particulièrement au passage du groupe au groupoïde. Par conséquent, on regardera les origines algébriques du concept de groupoïde ainsi que les apparitions du groupoïde fondamental chez Schreier, Reidemeister, Seifert-Threlfall, Bourbaki et d’autres. On analysera aussi le rôle du fait qu’on obtiendrait également un groupe/groupoïde sur l’ensemble des chemins d’un espace avec une certaine relation d’équivalence plus fine que l’homotopie.

Vendredi 21 octobre, matin, session Philosophie

9h30-11h Jean-Pierre Marquis (Univ. Montréal), Quelques remarques philosophiques sur la théorie de l’homotopie.

La théorie de l’homotopie touche à de nombreuses questions philosophiques fondamentales. Nous en aborderons deux. D’abord, il y a la question de l’identité. En effet, la théorie de l’homotopie repose sur une notion d’identité qui est radicalement différente de toutes les notions mathématiques qui ont été développées jusqu’ici. Cette notion pourrait bien avoir un impact fondamental non seulement sur les fondements des mathématiques, mais elle pourrait également être à la base de nouveaux cadres théoriques en métaphysique ou en philosophie du langage. Ensuite, il y a la question de l’accessibilité épistémologique aux types d’homotopie. En effet, on voit clairement dans l’évolution de la théorie que les mathématiciens doivent construire des modèles de ces derniers afin de mieux les comprendre, d’en saisir les propriétés. Ce qui nous intéresse ici au plus haut point, c’est la notion de modèle, qui n’a rien à voir avec les modèles tels qu’ils sont définis en logique, qui est à l’œuvre. Nous esquisserons ici quelques pistes de réflexions sur cette dimension fondamentale liée à la pratique des mathématiques.

11h15-12h45 Brice Halimi (Univ. Paris 10, SPHERE), Sur une application possible de la théorie de l’homotopie à la théorie des modèles.

Le lien entre logique et théorie de l’homotopie a été souligné par l’interprétation homotopique qui a été récemment proposée pour la théorie des types de Martin-Löf. J’essaierai de présenter un autre lien entre logique et théorie de l’homotopie, en montrant que le langage de la logique du premier ordre, et certaines notions élémentaires de théorie des modèles, se prêtent à une interprétation homotopique.

Vendredi 21 octobre, après-midi, session Mathématiques

14h15-15h45 Tim Porter (Univ. Wales, Bangor), Variations sur un thème d’homotopie.

Starting with the primitive notion of cylinder and homotopy (that will have been discussed in other talks) I will look at how via methods of Algebraic Homotopy and Homotopical Algebra one arrives at variants applicable to the proper homotopy context, prohomotopy and directed homotopy, and possibly the homotopy of evolving spaces.

16h-17h30 Sergei Soloviev (Univ. Toulouse Paul Sabatier, IRIT), Homotopy in foundations of mathematics (Voevodsky’s approach)

Recently there is a lot of activity around the ideas of Vladimir Voevodsky concerning the applications of homotopy to type theory and n-categories, as well as the uses of so called Univalence Axiom. The talk is a kind of survey of current activity in this domain including some subjective views on the perspectives of this approach.

Organisation : Sébastien Maronne (Univ. Toulouse Paul Sabatier, IMT), smaronne@math.univ-toulouse.fr

Avec le soutien de l’IMT, de la FREMIT et du GDR « Histoire des Mathématiques »