Cette semaine, ce sont les élèves de 1ère S du lycée Victor Hugo de Colomiers qui sont venus s’initier à la recherche à l’institut de mathématiques de l’université Paul Sabatier. Ils étaient ravis lorsqu’ils ont pris le bus en direction de l’université ! Leur thème de recherche les attendait : ce sera les nombres complexes.
Deux fonctions polynomiales
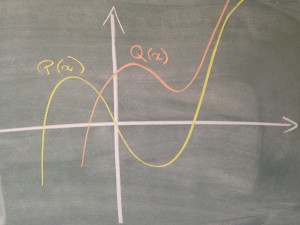
Les nombres complexes ont été introduits pour comprendre les zéros des polynômes. Sur le dessin à gauche, on voit le graphe de deux fonctions polynomiales de degré 3. Un exemple de telle fonction est donnée par l’application qui à un réel x associe le réel x³+x. Essayer de tracer cette fonction : pour x = 0, elle vaut 0³+0 = 0 ; pour x=1, elle vaut 1³+1 = 2 ; pour x=2, elle vaut 2³+2 = 10… et ainsi de suite. Sur le dessin, on voit que la courbe jaune coupe trois fois l’axe horizontal. Par contre, la courbe orange ne le coupe qu’une fois. Les nombres complexes permettent de comprendre ce que le dessin ne montre pas : les deux autres points où la courbe coupe l’axe horizontal.
Cercle trigonométrique et nombres complexes
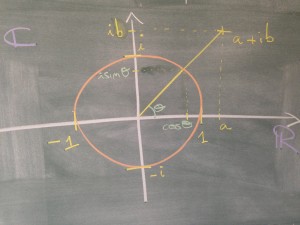
Dans les formules de Gerolamo Cardano et de Raphaël Bombelli, il y avait une quantité impossible : √-1. Connaissez-vous un nombre qui élevé au carré donne -1 ? S’il n’existe pas encore, ce n’est pas grave, on va le définir et l’appeler i. On aura alors i² = -1. Mais attention, il n’est pas le seul, on a aussi (-i)² = -1. Comment comprendre ce nombre ? Le dessin sur la droite va nous aider. Lorsque l’on part de 1, on peut arriver à -1 en faisant une rotation d’angle 180º et de centre 0. Une autre façon de faire, si on n’est pas sportif, est de commencer par une rotation de 90° et de centre 0, de faire une pause, puis de continuer avec une rotation de 90° de centre 0. Au final, on aura fait une rotation d’angle 180° et de centre 0. Voilà notre représentation géométrique de i, il correspond à une rotation d’angle 90° et de centre 0. Si on répète cette opération deux fois, on tombera sur -1.
Pendant trois jours, les élèves de Colomiers se sont creusés les méninges sur des questions abstraites à propos des nombres complexes. Ils ont ensuite présenté leurs travaux aux membres de l’institut de mathématiques à l’aide de posters sur les sujets suivants :
- les propriétés des nombres complexes,
- les relations entre les coefficients d’un polynôme et ses racines,
- les liens entre les nombres complexes et la trigonométrie,
- la méthode de Cardano et
- la résolution d’équations polynomiales de degré 3 particulières.
-
- Propriétés des nombres complexes
-
- Résolution d’une équation de degré 3 particulière
-
- Résolution d’une équation de degré 3 particulière
-
- Résolution d’une équation de degré 3 particulière
-
- Nombres complexes et trigonométrie
-
- Nombres complexes et trigonométrie
-
- Nombres complexes et trigonométrie
-
- Formule de Cardano
-
- Formule de Cardano
-
- Formule de Cardano
-
- Formule de Cardano
-
- Formule de Cardano
-
- Coefficients et racines de polynôme
Les vacances de Noël approchent. Avez-vous suffisamment bien travailler ?
La route des vacances
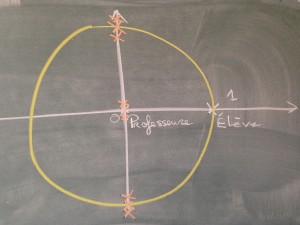
La professeure de la classe des 1ères S du lycée Victor Hugo veut empêcher ses élèves de partir en vacances. Pour cela, elle a installé des murs en orange sur la photo à gauche. La professeur est en 0 et les élèves en 1. Comment à l’aide de transformations obtenues avec les nombres complexes (et les nombres réels), les élèves peuvent-ils sortir de la classe en -1 et partir en vacances ? Aide : les nombres réels permettent de faire des déplacements sur les droites passant par 0 : par exemple, le nombre réel 2 permet de passer de 1 à 2 (on appelle ces transformations des homothéties) ; les nombres complexes qui sont sur le cercle jaune permettent de faire des déplacements sur le cercle centré en zéro et de rayon notre distance à 0 : par exemple, si on est en 1, le nombre complexe i permet de faire un quart de tour pour se trouver en i. Ceci étant dit, vous n’avez pas le droit passer en i car il y a un mur !