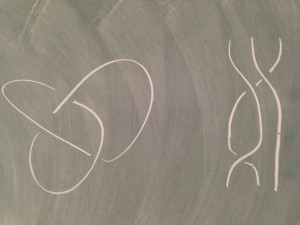Lycée Saint-Sernin (Toulouse) – Tresses et entrelacs

Lundi, 9h : les élèves du lycée Saint-Sernin arrivent à l’université Paul Sabatier de Toulouse. Leur professeur de mathématiques les emmène à l’institut de mathématiques où un enseignant-chercheur et trois doctorants sont là pour les accueillir. Le sujet sur lequel les élèves vont se casser la tête pendant trois jours est dévoilé : ce sera les tresses et les entrelacs.

Un sac de noeuds est là, il ne reste plus qu’à démêler les fils et à les ré-emmêler. Et ensuite, que peut-on faire avec toutes ces ficelles ? On définit la somme de deux noeuds en les mettant l’un à la suite de l’autre. De la même façon, on obtient le produit de deux tresses. Est-ce que la somme et le produit se comportent de la même façon que la somme et le produit des entiers pour lesquels on a :

• a + b = b + a et a . b = b . a, quels que soient les entiers a et b,
• (a + b) + c = a + (b + c) et (a . b) . c = a . (b . c), quels que soient les entiers a, b et c ?

Le noeud de trèfle et une tresse

Lorsque l’on dessine un noeud ou une tresse sur un tableau, on fait un choix de projection. Plusieurs dessins peuvent provenir du même noeud ou de la même tresse. Essayez par exemple de dessiner la tresse à droite avec uniquement un croisement.

À l’aide de ces dessins, appelés diagrammes de noeud, on cherche à voir si deux noeuds sont différents. Êtes-vous vraiment certains que le noeud de trèfle ne peut pas se démêler ?

Trois jours plus tard, les élèves de Saint-Sernin ont encore plein de questions mais aussi beaucoup de réponses. Ils les ont expliquées dans des posters qu’ils ont présentés aux membres de l’institut de mathématiques. Les thèmes étudiés étaient les suivants :

• somme de deux noeuds,
• produit de deux tresses,
• mouvements de Reidemeister,
• invariants de noeuds et tresses,
• l’implémentation des noeuds dans un ordinateur et la recherche d’algorithme de comparaison de noeuds,
• nombre d’entrelacements et
• un problème de miroirs (que fait ce thème ici ? la réponse est à chercher du côté des groupes de Coxeter…).