Lycée Françoise (Tournefeuille) – Géométries

Le stage hippocampe, d’initiation à la recherche pour les lycéens, accueille cette semaine les élèves de première S du lycée Françoise de Tournefeuille. Après un court trajet en bus, les élèves arrivent à l’université où ils découvrent le thème : géométries. Le « s » à la fin est important. Les élèves ne se sont pas contenter de faire de la géométrie comme Euclide en a fait 300 ans avant J.C.. Ils ont aussi découvert et réfléchi sur les autres géométries inventées par les mathématiciens depuis : géométrie sphérique, géométrie hyperbolique, géométrie projective…

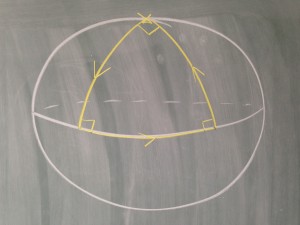Jetons un coup d’oeil à la géométrie sphérique en se plaçant sur la Terre : disons que vous partez du pôle Nord, parcourez ensuite un quart du globe de façon à atteindre l’équateur, déplacez-vous ensuite vers l’Est de façon à parcourir à nouveau un quart du globe et finissez en remontant vers le pôle Nord. En regardant les angles définis par les tangentes des courbes tracées sur la Terre, on remarque que le triangle obtenu possède trois angles droits. Bizarre. N’avez-vous pas appris que la somme des angles d’un triangle doit être égale à 180° ?

Pour étudier les triangles, les carrés ou les autres formes dessinées sur la sphère, il faut donc travailler avec des résultats différents et modifier son intuition. Il est aussi possible de définir une géométrie dans laquelle la somme des angles d’un triangle est inférieur à 180°. Elle s’appelle la géométrie hyperbolique. Elle peut paraître artificielle mais elle est tout aussi utile que les autres, si ce n’est plus. Pour vous en convaincre, jetez un coup d’oeil aux vidéos vulgarisées sur la relativité proposées par Lê sur son blog. La douzième vidéo porte sur la géométrie hyperbolique.

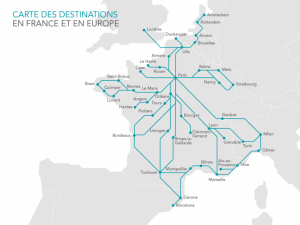Le géomètre mesure aussi des distances. On a presque tous entendu parler de la distance euclidienne qui se calcule en prenant la racine carrée de la somme des carrées des coordonnées (ouf !).  Elle nous permet de mesurer des distances dans le plan mais ne convient plus sur la sphère ou en géométrie hyperbolique. Mais ce ne sont pas les seuls exemples d’espaces avec distance (le terme mathématique est « espace métrique »). En effet, lorsqu’on se promène sur la Terre en voiture ou en train, on ne peut pas toujours suivre les ligne droite de la sphère car on est contraint par les routes et les voies ferrées. On peut alors définir tout un tas de distances en fonction des problèmes que l’on considère.

Pendant les trois jours du stage, les élèves du lycée Françoise ont cherché à démêler les droites euclidiennes des droites sphériques ou des droites hyperboliques et ça n’a pas été facile ! Ils ont finalement écrits de beaux posters sur les sujets suivants :

• la formule d’Euler,
• les solides de Platon,
• le jeux Double,
• les ours,
• New York et Paris,
• la géométrie hyperbolique,
• les arbres métriques, et
• la comparaison de photos en noir et blanc.

Comme on le voit sur la première photo, il est possible de tracer un triangle ayant trois angles droits sur la sphère. Savez-vous tracer un carré dont la somme des angles vaut 3π ? Vous avez le long weekend pour trouver la solution !