Les élèves de première S du lycée Saint-Sernin sont venus à l’institut de mathématiques de Toulouse les 9, 10 et 11 mars pour participer à un stage hippocampe, d’initiation à la recherche. Le sujet de la semaine était bien mystérieux : les nombres (ir)rationnels et les fractions continues.
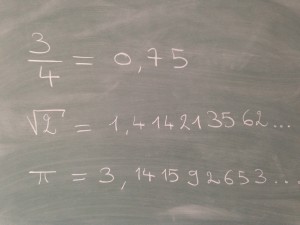 Un nombre rationnel est une fraction, par exemple 3/4. Par opposition, un nombre irrationnel est un nombre qui ne peut pas se mettre sous la forme d’une fraction de deux nombres entiers. Les premiers exemples de nombres irrationnels auxquels on peut penser sont √2 ou π. Il n’est pas forcément évident de montrer qu’ils sont irrationnels mais c’est un bon exercice de s’essayer sur √2.
Un nombre rationnel est une fraction, par exemple 3/4. Par opposition, un nombre irrationnel est un nombre qui ne peut pas se mettre sous la forme d’une fraction de deux nombres entiers. Les premiers exemples de nombres irrationnels auxquels on peut penser sont √2 ou π. Il n’est pas forcément évident de montrer qu’ils sont irrationnels mais c’est un bon exercice de s’essayer sur √2.
Une manière de décrire un nombre est d’utiliser sa décomposition décimale. Cependant, il arrive que cette décomposition soit infinie. C’est le cas pour les nombre irrationnel mais aussi pour certains nombres rationnels comme 1/3 ou 2/7. Dans ce stage, les élèves du lycée Saint-Sernin ont découvert une autre façon de décrire les nombres : à l’aide des fractions continues.
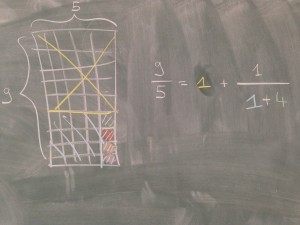 Il est facile de comprendre comment fonctionnent les fractions continue sur les nombres rationnels. Si vous cherchez la fraction continue associée au nombre 9/5, il vous suffit de dessiner un carré de 9 par 5. Retirer ensuite le plus grand carré possible : ici, ce sera un carré de 5*5. Réitérer cette opération : le prochain carré sera de 4*4. Pour les quatre prochaines étapes, vous trouverez des carrés de taille 1*1. La fraction continue associée à 9/5 est donc 1+1/(1+4). À vous : pouvez-vous donner la fraction continue associée à la fraction 8/5 ?
Il est facile de comprendre comment fonctionnent les fractions continue sur les nombres rationnels. Si vous cherchez la fraction continue associée au nombre 9/5, il vous suffit de dessiner un carré de 9 par 5. Retirer ensuite le plus grand carré possible : ici, ce sera un carré de 5*5. Réitérer cette opération : le prochain carré sera de 4*4. Pour les quatre prochaines étapes, vous trouverez des carrés de taille 1*1. La fraction continue associée à 9/5 est donc 1+1/(1+4). À vous : pouvez-vous donner la fraction continue associée à la fraction 8/5 ?
Passons maintenant aux nombres irrationnels et basons-nous sur la même idée. Considérons un rectangle de côtés 1 et π. Le plus grand carré que l’on peut retirer de ce rectangle est un carré de taille 1*1, et on pourra en retirer 3 de cette taille. En continuant comme précédemment, on trouve alors la fraction continue associée à π. Les fractions continues permettent d’approcher très efficacement les nombres par des fractions.
Pendant trois jours, les premières S de Saint-Sernin ont formalisé et étudié plus en détail la notion de fraction continue. Ils ont ensuite préparé des posters pour les présenter aux membres de l’institut de mathématiques sur les sujets suivants :
- convergence des fractions continues ;
- monotonie de cette convergence ;
- qualité de l’approximation donnée par une fraction continue ;
- l’incommensurabilité de la diagonale ;
- la périodicité dans les développements décimaux ou en fraction continue.
- Convergence
- Convergence
- Convergence
- Convergence
- Convergence
- Convergence
- Monotonie
- Approximation
- Approximation
- Approximation
- Approximation
- Incommensurabilité
- Incommensurabilité
- Incommensurabilité
- Développement décimal
- Périodicité
- Périodicité
- Périodicité
- Périodicité
- Approximation
- Approximation
- Approximation
- Approximation
Pour aller plus loin : supposer acquis le résultat de John Wallis suivant
π/2 = 2*∏(1-1/(2i+1)²),
où le produit ∏ est sur tous les i≥1. En déduire la fraction continue associée à 4/π. Vous serez alors surpris de découvrir une formule très simple donnant une très bonne approximation du nombre irrationnel 4/π.























