Lycée Françoise (Tournefeuille) – Permutations

Mardi 10 janvier 2017. Depuis la veille l’eau a envahi la station de métro de Saint-Agne. Chacun arrive comme il peut à l’Université Paul Sabatier, qui à pied, qui en bus à travers les embouteillages… C’est donc avec un peu de retard que les élèves de 1°S du lycée Françoise de Tournefeuille accompagnés de leurs professeurs arrivent pour participer à leur stage Hippocampe. Un enseignant-chercheur les attend pour leur expliquer les bases de leur thème de recherche  : les permutations sur des ensembles finis.

Il s’agit pour eux d’une découverte. Permutations et dénombrements ont disparu depuis quelques années des programmes du lycée. Comment compter le nombre de façons d’ordonner les éléments d’un ensemble ?
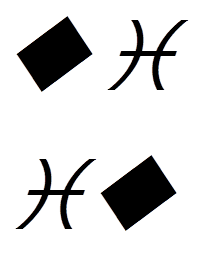Il n’est pas difficile de voir qu’il y a 2 façons de le faire lorsque l’ensemble a deux éléments, et qu’il y en a 6 pour un ensemble de trois éléments.

Ce sont les permutations de ces ensembles. Les élèves découvrent ainsi les factorielles : le calcul 3 x 2 x 1 qui permet de compter le nombre de permutations d’un ensemble à 3 éléments se note : 3! (factorielle 3).

Et ainsi de suite… Le nombre de permutations d’un ensemble à n éléments est égal à
n x (n-1) x (n-2) x … x 2 x 1 = n!

Notation d’un cycle de trois éléments

Ils découvrent ensuite les transpositions, permutations très simples qui échangent deux éléments de l’ensemble en laissant les autres invariants. Puis les cycles, ou permutations circulaires, qui font « tourner » certains éléments en laissant les autres invariants.
Une transposition est un cycle de deux éléments.

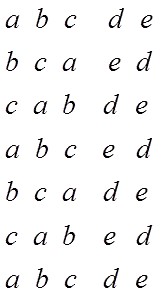Prenons un exemple. Faisons agir sur l’ensemble de 5 éléments
{a, b, c, d, e} la permutation notée  : (a, b, c) (d, e).
Voyez ci-contre ce que nous obtenons au fur et à mesure :
a, b et c tournent entre eux, d et e  font de même. Nous constatons qu’il nous faut faire agir 6 fois de suite la permutation pour que tous les éléments retrouvent leur place d’origine. La période de cette permutation est égale à 6.

Les élèves apprennent aussi que toutes les permutations d’un ensemble fini peuvent se décomposer en un produit de cycles.

Il existe des utilisations amusantes de la théorie des permutations.
Le jeu de Taquin consiste, en utilisant la case laissée libre, à déplacer les petites 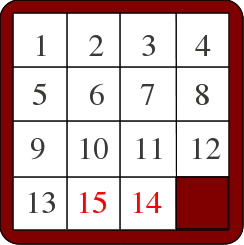plaques coulissantes d’un cadre (comme celui qui figure ci-contre) pour ranger les nombres dans l’ordre croissant. Par exemple, dans le cas de la figure ci-contre, il faudrait réussir en faisant coulisser les cases à inverser les places de 14 et 15. L’étude des permutations permet de montrer que cela est impossible.

C’est également une étude de permutations qui peut nous permettre de connaître le nombre de configurations possibles du fameux Rubik’s Cube. Ce nombre est considérable, plus de 43 milliards de milliards !

Les élèves se sont complètement pris au jeu de la recherche, même si les questions posées étaient difficiles, même si la fatigue se faisait parfois sentir en fin de journée ! Le dernier après-midi du stage, ils ont exposé les posters qu’ils avaient réalisé  le matin même pour résumer leur travail. Les enseignants-chercheurs de l’institut de mathématiques ont pu leur poser des questions sur :

• l’étude des profils d’une permutation
• un puzzle avec deux cycles emboîtés
• une étude d’addition et de multiplication en rapport avec l’arithmétique
• la recherche de la plus longue période possible pour les permutations d’un ensemble donné
• une étude des dérangements
• la période moyenne d’un point.

Considérons les nombres de 1 à 2018 rangés dans l’ordre croissant. Parmi les permutations proposées ci-dessous, saurez-vous dire lesquelles, répétées, permettent de ranger les nombres dans l’ordre inverse ?

1. On peut permuter entre eux deux nombres arbitraires.
2. On peut permuter entre eux deux nombres voisins.
3. On peut permuter entre eux deux nombres à condition qu’ils ne soient séparés que par un seul nombre.
4. On peut permuter deux nombres à condition qu’entre eux il y ait exactement deux nombres.
5. On peut choisir trois nombres et appliquer entre eux une permutation circulaire.