Le mercredi 25 janvier, les 30 élèves d’une classe de terminale S du lycée Saint-Exupéry arrivent à l’Université Paul Sabatier pour participer à un stage Hippocampe. Ils viennent s’initier pendant trois jours aux joies et aux difficultés de la recherche. Leur professeur de mathématiques, un enseignant-chercheur et trois doctorants sont là pour les aider si besoin dans ce travail.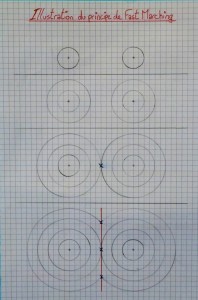
Le thème du stage paraît familier à première vue : les distances. Mais quand le plus court chemin d’un point à un autre n’est pas la ligne droite, tout se complique !
Traçons des ensembles de points tous situés à la même distance d’un point donné. Nous obtenons des courbes appelées courbes « d’isodistance ». Dans le cas classique, comme sur la figure ci-contre, ces ensembles sont des cercles. Les élèves ont obtenu la médiatrice de deux points donnés (tracée en rouge), par la méthode du « Fast Marching ».
 Mais si les courbes d’isodistance ne sont pas des cercles, comme par exemple les courbes de relief en montagne, la médiatrice n’est plus une droite. Sur la figure ci-contre, les élèves ont indiqué les courbes situées aux mêmes distances 1, 2, 3… de chacun de deux points donnés A et B. Quand deux courbes portant le même numéro ont un ou plusieurs points en commun, nous obtenons des points de la médiatrice.
Mais si les courbes d’isodistance ne sont pas des cercles, comme par exemple les courbes de relief en montagne, la médiatrice n’est plus une droite. Sur la figure ci-contre, les élèves ont indiqué les courbes situées aux mêmes distances 1, 2, 3… de chacun de deux points donnés A et B. Quand deux courbes portant le même numéro ont un ou plusieurs points en commun, nous obtenons des points de la médiatrice.
D’autre part, les élèves se sont appliqué à montrer que le chemin le plus court pour aller du point A au point B (chemin tracé sur la figure) passe par les points de tangence de deux courbes d’isodistance.
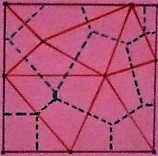
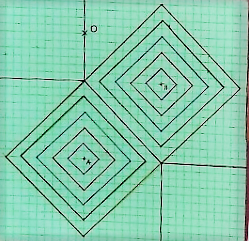 Imaginons maintenant que nous nous déplaçons dans une ville quadrillée de rues rectilignes et perpendiculaires les unes aux autres, entourant des pâtés d’immeubles. Les élèves ont utilisé des feuilles de papier quadrillé pour modéliser la situation. Ils ont cherché et tracé les courbes d’isodistance sur ces grilles cartésiennes où il n’est possible de se positionner que sur les lignes des quadrillages. Ces courbes d’isodistance sont des points situés sur des carrés (on ne peut pas se déplacer sur les diagonales du quadrillage, chaque petit carré représentant un « immeuble »).
Imaginons maintenant que nous nous déplaçons dans une ville quadrillée de rues rectilignes et perpendiculaires les unes aux autres, entourant des pâtés d’immeubles. Les élèves ont utilisé des feuilles de papier quadrillé pour modéliser la situation. Ils ont cherché et tracé les courbes d’isodistance sur ces grilles cartésiennes où il n’est possible de se positionner que sur les lignes des quadrillages. Ces courbes d’isodistance sont des points situés sur des carrés (on ne peut pas se déplacer sur les diagonales du quadrillage, chaque petit carré représentant un « immeuble »).
Avec cette contrainte, saurez-vous dire si le point appelé D sur la figure ci-contre est plus près de A ou de B ?
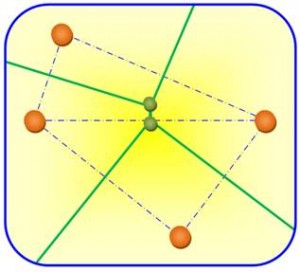
Revenons à nos médiatrices. Étant donnés deux points dans le plan, la droite qui est à égale distance de ces deux points, la médiatrice, divise le plan en deux régions, chacune de ces régions contenant les points qui sont plus proches de l’un des points choisis au départ que de l’autre. Lorsqu’on ajoute des points, le même principe s’applique, et on obtient des cellules contenant les points plus proches de l’un des points fixés que de tous les autres. L’ensemble de ces cellules forment un diagramme de Voronoï dans le plan.
Les élèves vont ensuite tracer la triangulation de Delaunay : il s’agit de former un pavage (« partition ») de la surface délimitée par les points donnés à l’aide de triangles, de manière à ce que le cercle circonscrit à chacun de ces triangles ne contienne aucun autre des points donnés au départ.
On montre que, parmi toutes les triangulations possibles, celle de Delaunay maximise les plus petits angles. De cette manière, elle donne les triangles les moins aplatis possibles.
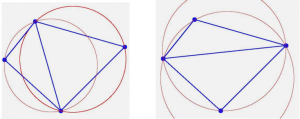 Sur la figure de gauche, il s’agit d’une triangulation de Delaunay pour 4 points. Par contre, à droite, le 4ème point appartient aux cercles circonscrits aux triangles, il ne s’agit pas d’une triangulation de Delaunay.
Sur la figure de gauche, il s’agit d’une triangulation de Delaunay pour 4 points. Par contre, à droite, le 4ème point appartient aux cercles circonscrits aux triangles, il ne s’agit pas d’une triangulation de Delaunay.
Pour un nombre important de points, l’utilisation d’algorithmes devient nécessaire autant pour la construction de plus courts chemins que pour celle de cellules de Voronoï et de triangulations de Delaunay. Ce fut l’occasion pour les élèves de bâtir certains algorithmes.
Il existe de nombreuses applications à ces notions : déplacements de robots, étude de l’évolution de cellules cancéreuses, détermination de frontières sous-marines entre pays voisins, modélisation de réseaux téléphoniques, étude de la croissance des plantes…

On a même montré que le motif de la robe des girafes réticulées correspond avec une approximation satisfaisante à des cellules de Voronoï, explications à l’appui…
Après un travail intense, passionnant et souvent passionné, le dernier jour du stage a été consacré à la confection de posters. Les élèves ont ainsi exposé leurs résultats et les membres de l’institut de mathématiques ont pu leur poser des questions au sujet :
- des plus courts chemins et de l’inégalité triangulaire,
- de déplacements dans les grilles cartésiennes,
- des graphes,
- de la triangulation de Delaunay,
- du trajet d’un rayon lumineux dans une fibre,
- du principe de Fermat.
- Inégalité triangulaire et courbes d’isodistance
- Inégalité triangulaire et courbes d’isodistance
- Principe du Fast Marching
- Grille cartésienne et Fast Marching
- Grille cartésienne et Fast Marching
- Application aux graphes
- Triangulation de Delaunay
- Triangulation de Delaunay, 1
- Triangulation de Delaunay, 2
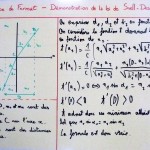
- Principe de Fermat et loi de Snell-Descartes
- La fibre optique
- La fibre optique
Et à propos de triangles…
- Sauriez-vous inscrire un triangle équilatéral dans un carré de façon symétrique par rapport à une des diagonales de ce carré ?
- Et sauriez-vous construire un carré circonscrit de façon symétrique autour d’un triangle équilatéral ?