Lycée Claude Nougaro (Caussade) – Des coniques

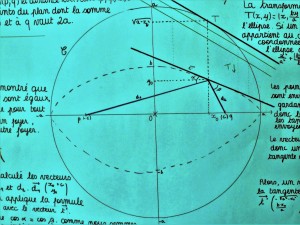
19 avril 2017.  Un autobus transportant trente-cinq jeunes gens d’une classe de 1ère S et quelques-uns de leurs professeurs, en provenance de Caussade, s’arrête à l’Université Paul Sabatier. Les uns sont élèves et les autres enseignants du lycée Claude Nougaro de cette ville. Ces élèves viennent s’initier pendant trois jours à la recherche en mathématiques sous la férule d’un enseignant-chercheur. Deux doctorants sont là également pour les soutenir pendant ces journées dans leur travail de recherche.

Les apprentis chercheurs découvrent rapidement quel sera leur thème de recherche : les coniques.
Voilà qui est (presque) nouveau pour ces élèves ! Certes, ils ont travaillé au lycée avec des paraboles, en tant que représentations de fonctions de degré 2. Ils ont aussi rencontré en seconde quelques hyperboles, représentations de fonctions homographiques. Mais l’étude plus approfondie des propriétés des coniques a disparu des programmes de lycée, et en particulier l’étude des ellipses.
Tout commence par des définitions, et voici celles qui leur sont données pour ellipses et hyperboles. Elles concernent la distance des points de la conique à leurs foyers. La somme des distances d’un point de l’ellipse à ses deux foyers est constante. Pour l’hyperbole, c’est la différence de ces deux distances qui est constante.

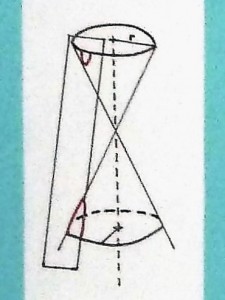
Hyperbole en rouge

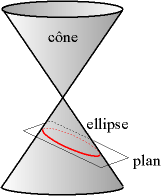
Au travail ! Un peu de géométrie dans l’espace pour commencer. Partant des définitions ci-dessus, il va falloir étudier la section d’un cône par un plan, et montrer que, suivant l’inclinaison de ce plan cette section peut parfois être une ellipse… ,

parfois une hyperbole…

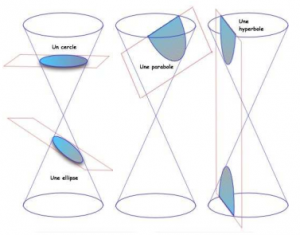Toujours selon l’inclinaison du plan, l’intersection avec le cône peut aussi être une parabole. Les élèves n’auront pas à étudier ce cas.

La voilà, l’origine du mot « conique » !

Pour arriver à prouver ces résultats, les élèves vont devoir démontrer quelques propriétés géométriques des cercles et triangles, pour certaines quelque peu oubliées… Ils ont besoin de bissectrices pour obtenir le cercle inscrit dans un triangle, utilisent des tangentes à un cercle, ou encore le théorème de Pythagore pour montrer des égalités de longueur…

Une autre manière d’aborder ellipses et hyperboles : les définir au moyen d’équations après avoir choisi le repère dans lequel travailler. Voilà encore une occasion d’utiliser le théorème de Pythagore, et en avant pour les calculs !

Déterminer une expression du cosinus d’un angle quelconque dans un triangle se révèle nécessaire pour aborder ensuite les  propriétés im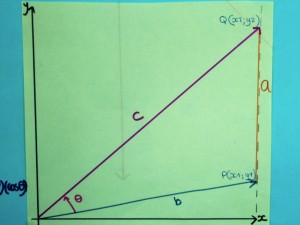portantes de réflexion dans une ellipse et dans une parabole. Un groupe d’élèves est à la recherche de cette expression et doit pour cela utiliser des notions récemment vues en classe, notions de trigonométrie, de vecteurs directeurs de droites. Ils rencontrent même au passage la propriété d’Al Kashi, généralisation du théorème de Pythagore à un triangle quelconque.

Réflexivité dans l’ellipse

Un autre groupe aborde la propriété de réflexivité dans une ellipse. Cette propriété importante nous dit que si un rayon passe par l’un des foyers de l’ellipse, alors il passera par l’autre foyer après avoir été réfléchi par l’ellipse.
Une propriété bien utile en optique : plaçons une source lumineuse sur l’un des deux foyers, après reflexion les rayons lumineux se concentreront sur l’autre foyer.
Ou bien en acoustique : dans un lieu de forme elliptique, un son même faible émis de l’un des foyers est bien perçu par une personne se trouvant à l’emplacement de l’autre foyer. Cette propriété est connue depuis des siècles.

Chambre à écho

Des salles de l’abbaye de La Chaise Dieu pouvaient ainsi servir à la confession des lépreux, sans que le confesseur ait besoin d’approcher ces derniers. Les chuchotements émis par le lépreux à l’endroit d’un foyer étaient clairement perçus par le confesseur placé en l’autre foyer, et pas ailleurs…

Dans le métro parisien aussi, deux personnes situées aux deux foyers de la voûte elliptique peuvent converser d’un quai à l’autre sans être entendues.

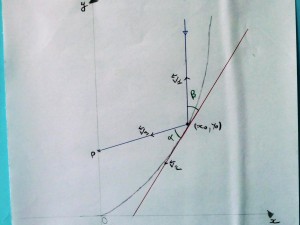
Réflexivité dans la parabole

Pour démontrer la propriété de réflexivité d’une parabole, comme pour démontrer celle de l’ellipse,  les élèves se lancent dans de longs calculs dans le but d’établir des égalités d’angles. Ces égalités  permettront ensuite d’utiliser la loi de Snell-Descartes et de prouver qu’un rayon parallèle à l’axe de la parabole se réfléchit sur son foyer.
Cette propriété a de multiples applications, à commencer  par l’existence des antennes paraboliques. Il s’agit en fait de paraboloïdes, obtenus par révolution d’une parabole autour de son axe. Un paraboloïde peut être un émetteur aussi bien qu’un récepteur. Les rayons parallèles à l’axe sont concentrés au point focal. Réciproquement, des rayons émis depuis ce point focal sont renvoyés en un faisceau de rayons parallèles. Cette double fonctionnalité permet d’utiliser des paraboloïdes comme relais hertziens dans des régions accidentées où la télévision et la téléphonie mobile ne passeraient pas.

Les coniques nous concernent de bien des manières… sans oublier notre Terre qui décrit dans l’espace une ellipse dont un des foyers est le Soleil. Sans oublier les orbites variées des comètes. Orbites elliptiques pour celles qui repassent de manière prévisible sous nos yeux… ou ceux de nos descendants. Paraboliques, hyperboliques pour d’autres, qui ne reviendront jamais…

Vendredi, début d’après-midi. La matinée a été consacrée à la fabrication de posters. Les élèves accrochent maintenant les posters dans le hall du bâtiment de mathématiques. Enseignants-chercheurs et doctorants ne vont pas tarder à venir lire leurs travaux, et leur poser des questions à ce sujet…
Place aux travaux des élèves :

Allez, encore deux petites questions ! Saurez-vous retrouver et expliquer la méthode dite « méthode du jardinier » pour tracer une ellipse ?
Et saurez-vous trouver une méthode analogue pour tracer une hyperbole ?

Les élèves du lycée Nougaro ont aussi fait parlé d’eux et du stage hippocampe dans la presse ici.