Introduction

Immeubles

Contemplons la définition suivante d’immeuble :

Définition Un immeuble est un complexe simplicial \(\Delta\) obtenu comme union de sous-complexes \(\Sigma\) (les appartements) satisfaisant les axiomes suivants:

1. Chaque appartement \(\Sigma\) est un complexe de Coxeter.
2. Pour tout couple de simplexes \(A, B \in \Delta\), il existe un appartement \(\Sigma\) contenant les deux.
3. Si \(\Sigma\) et \(\Sigma’\) sont deux appartements contenant des simplexes \(A\) et \(B\), alors il existe un isomorphisme \(\Sigma \to \Sigma’\) fixant \(A\) et \(B\) point par point.

Dans ces exposés on va introduire la notion de complexe de Coxeter, qui sont des complexes simpliciaux basiques qui serviront à contruire les immeubles.

Les axiomes ci-dessus disent qu’un immeuble est en un certain sens un objet très symétrique, on verra plus tard leurs conséquences. Noter cependant qu’il est possible qu’un immeuble n’admette aucun automorphisme non trivial, comme dans l’exemple suivant :

Exemple Soit \(\Delta\) un arbre simplicial, dont tous les sommets sont de valences \(\ge 3\) deux à deux distinctes. Alors \(\Delta\) est un immeuble, dont les appartements sont les droites simpliciales plongées dans \(\Delta\).
On verra que ce sont des complexes de Coxeter de type \(\tilde A_1\).

Groupes et matrices de Coxeter

Un groupe de Coxeter \(W\) est un groupe engendré par un ensemble \(S\) (disons fini, de cardinal \(n\)) d’involutions, et qui admet une présentation par générateurs et relations très simple :
\[
W = \left\langle S \mid (s,t)^{m(s,t)} = 1\right\rangle
\]
Ici la matrice \(M = (m(s,t))_{1 \le s,t \le n}\) est symétrique à coefficients entiers positifs, avec des \(1\) sur la diagonale est des entiers \(\ge 2\) partout ailleurs. On admet aussi la valeur \(m(s,t) = \infty\). On dit que \(M\) est la matrice de Coxeter encodant \(W\). Si on veut souligner le choix de \(S\), on parle de système de Coxeter \((W,S)\).

Exemple

1. Le groupe \(S_3\) des symétries d’un triangle équilatéral, engendré par les transpositions \((12)\) et \((23)\) dont le produit est d’ordre 3.
2. Le groupe infini engendré par les symétries par rapport aux côtés d’un
   triangle équilatéral, dont les produits deux à deux sont d’ordre 3.
3. Le groupe \(\mathrm{PGL}_2({\mathbb Z})\) est engendré par les matrices
   \[
   s_1 = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \quad
   s_2 = \begin{pmatrix} -1 & 1 \\ 0 & 1 \end{pmatrix}, \quad
   s_3 = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}.
   \]
   et les produits \(s_1s_2\), \(s_1s_3\), \(s_2s_3\) sont d’ordre respectif \(3,2,\infty\).

Graphes de Coxeter

La donnée d’une telle matrice \(n \times n\) est encodée par un graphe de Coxeter \(\Gamma\), avec \(n\) sommets et une arête avec étiquette \(m(s,t)\) pour chaque \(m(s,t) \ge 3\). Il est d’usage de ne pas noter les étiquettes 3 sur les dessins. On dit que la matrice de Coxeter \(M\) est irréductible (ou indécomposable) si le graphe \(\Gamma\) associé est connexe.

La matrice de Gram d’un graphe de Coxeter est la matrice symétrique \(A\) avec coefficients \(-\cos \frac{\pi}{m(s,t)}\) (à interpréter comme \(-1\) dans le cas \(m(s,t) = \infty\)). Pour les calculs il est souvent plus aisé de considérer \(2A\) (notamment pour que les \(-\cos \frac{\pi}{3}\) deviennent des \(-1\)…)

Si \(\Gamma\) est un graphe de Coxeter, on notera \(\det (\Gamma)\) le déterminant \(\det (2A)\), où \(A\) est la matrice de Gram associée.

Exemple
Groupe \(W\) d’ordre 48 des isométries de \({\mathbb R}^3\) préservant un cube:

• \( M = \left(\begin{array}{ccc} 1 & 3 & 2 \\ 3 & 1 & 4 \\ 2 & 4 & 1 \end{array}\right)\)
• \(\Gamma = \)
• \( 2A = \left(\begin{array}{ccc} 2 & -1 & 0 \\ -1 & 2 & -\sqrt 2 \\ 0 & -\sqrt 2 & 2 \end{array}\right) \)
• \(\det (\Gamma) = 2 \).

Représentation canonique

Soit \((W,S)\) un système de Coxeter, \(V\) l’espace vectoriel \(V = \oplus_{s \in S} {\mathbb R} e_s\), et \(B(.,.)\) la forme bilinéaire définie par
\[
B(e_s,e_t) = – \cos \frac{\pi}{m(s,t)}.
\]
On fait agir \(W\) sur \(V\) en posant, pour chaque \(s \in S\)
\[\sigma_s(v) = v – 2 B(e_s,v) e_s,\]
ou autrement dit \(\sigma_s\) est la (une) réflexion orthogonale de plan
\(e_s^\perp\) par rapport à la forme \(B\).
Par acquis de conscience, on peut vérifier que pour tout \(v,v’ \in V\), on a :
\[\begin{array}{rl}
B(\sigma_s (v), \sigma_s (v’) ) &= B(v-2B(e_s,v)e_s, v’-2B(e_s,v’)e_s) \\
&= B(v,v’) – 2 B(e_s,v) B(e_s,v’) – 2 B(e_s,v’)B(v,e_s) +4 B(e_s,v)B(e_s,v’)\cdot 1
\\
&= B(v,v’).
\end{array}\]
On obtient donc un morphisme de \(W\) vers le groupe orthogonal \(\mathrm O(V)\) pour la forme \(B\).

Lemme
Soit \(W = \langle S; (st)^{m(s,t)} = 1 \rangle\) un groupe de Coxeter. Alors chaque \(s \in S\) est d’ordre 2 dans \(W\), et chaque produit \(st\) est d’ordre \(m(s,t)\).

Démonstration :
On a un morphisme signature \(W \to \{\pm 1\}\) qui envoie chaque \(s \in S\) sur \(-1\), donc les \(s\) sont d’ordre 2 dans \(W\). Si \(s\neq t \in S\), alors \(\sigma_s\) et \(\sigma_t\) préserve le plan \(\mathrm{Vect}(e_s, e_t)\), et comme la restriction de \(B\) est de matrice définie positive (on traite d’abord le cas \(m = m(s,t)\) fini)
\[
\begin{pmatrix}
1 & -\cos \frac{\pi}{m} \\ -\cos \frac{\pi}{m} & 1
\end{pmatrix},
\]
le groupe \(\langle \sigma_s, \sigma_t \rangle\) est diédral d’ordre \(m\), car l’angle entre les deux vecteurs \(e_s\) et \(e_t\) est \(\pi – \frac{\pi}{m}\). Cela montre que \(st\) est d’ordre \(m\) dans \(W\).

Représentation duale

On part de l’action de \(W\) sur \(V’ = \oplus_{s \in
S} {\mathbb R} e_s\), par
\[s'(f) = f – 2 B(e_s,f) e_s\]
On note \(V\) le dual de \(V’\).
On pense aux éléments de \(V’\) comme des formes linéaires, et à ceux de \(V\) comme des vecteurs.
Pour tout \(s \in S\), il existe un unique vecteur \(v_s \in V\) tel que pour tout \(f \in V’\),
\[ f(v_s) = B(e_s,f). \]

Lemme
L’action duale de \(S\) sur \(V\) est donnée par
\[
s(v) = v-2e_s(v) v_s.
\]

Démonstration :
\[\begin{array}{rl}
\langle e_t, s(v) \rangle
&= \langle e_t, v- 2 e_s(v) v_s \rangle \\
&= e_t(v) – 2 e_t(v_s) e_s(v) \\
&= e_t(v) – 2B(e_s,e_t)e_s(v) \\
&= \langle e_t – 2B(e_s,e_t)e_s,v \rangle \\
&= \langle s'(e_t), v \rangle.
\end{array}\]

Exemple
Soit \(W\) le groupe diédral infini:

• \( M = \begin{pmatrix} 1 & \infty \\ \infty & 1 \end{pmatrix} \)
• \(\Gamma = \)
• \(A = \begin{pmatrix} 1 & -1 \\ -1 & 1 \end{pmatrix} \)
• \( \det (\Gamma) = 0 \).

On considère l’espace vectoriel \(V’ = {\mathbb R} e_s \oplus {\mathbb R} e_t\), et \(V\) son dual. On définit comme précédemment deux réflexions \(s’\) et \(t’\) sur \(V’\):
\[\begin{array}{c}
s'(f) &= f – 2B(e_s,f)e_s, \\
t'(f) &= f – 2B(e_t,f)e_t.
\end{array}\]
Observer que \(s'(e_s) = -e_s\), \(t'(e_t) = -e_t\) et \(s’,t’\) fixent toutes deux point par point la droite engendrée par \(e_s + e_t\), ce qui donne :
\[\begin{array}{cc}
s'(e_t) = 2e_s + e_t, && t'(e_s) = e_s + 2e_t.
\end{array}\]

Notons \(s,t\) les réflexions linéaires sur \(V\) induites par \(s’,t’\), alors en notant \((x,y)\) les coordonnées sur \(V\) telles que
\[\begin{array}{cc}
e_s(x,y) = x, && e_t(x,y) = -x + y,
\end{array}\]
on obtient
\[\begin{array}{cc}
s (x,y) = (-x,y), && t(x,y) = (-x + 2y, y).
\end{array}\]
En effet :
\[\begin{array}{ccccccccccccccccc}
\langle e_s, s(s,y) \rangle &&=&&\langle e_s, (-x,y) \rangle&& = &&-x &&=&& \langle -e_s, (x,y) \rangle &&=&& \langle s'(e_s), (x,y) \rangle, \\
\langle e_t, s(s,y) \rangle &&=&& \langle e_t, (-x,y) \rangle&& = &&x + y &&=&& \langle 2e_s+e_t, (x,y) \rangle &&= &&\langle s'(e_t), (x,y) \rangle, \\
\langle e_s, t(x,y) \rangle &&=&&\langle e_s, (-x+2y,y) \rangle&& = &&-x+2y &&=&& \langle e_s+2e_t, (x,y) \rangle &&=&& \langle t'(e_s), (x,y) \rangle, \\
\langle e_t, t(x,y) \rangle &&=&&\langle e_t, (-x+2y,y) \rangle&& = &&x-y &&=&& \langle -e_t, (x,y) \rangle &&=&& \langle t'(e_t), (x,y) \rangle.
\end{array}\]

Le cas \(W\) fini

Théorème
Soit \((W,S)\) un système de Coxeter, et \(B\) la forme quadratique associée. Le groupe \(W\) est fini si et seulement si la forme \(B\) est définie positive.

Démonstration :
On peut se ramener à \((W,S)\) irréductible, en travaillant sur chaque bloc de la matrice de \(B\).

Si \(B\) est définie positive, \(W\) s’identifie à un groupe discret du groupe
compact \(O(V)\), et est donc fini.

Réciproquement si \(W\) est fini, par moyennisation du produit scalaire standard
sur \(V\) il préserve un produit scalaire. On a donc deux formes bilinéaires invariantes, \(B\) et un produit scalaire \(\langle \cdot, \cdot \rangle\). On veut montrer que \(B = c\, \langle \cdot, \cdot \rangle\) pour une constante \(c > 0\). Tout d’abord \(B\) est non dégénérée, car sinon \(\ker B\) serait un sous-espace stable sans supplémentaire stable. Tout sous-espace stable devrait être dans le noyau de \(B\), donc la représentation de \(W\) est irréductible. Le centralisateur de \(W\) est réduit aux matrices scalaires. Cela implique qu’il existe une unique forme bilinéaire symétrique invariante (à un scalaire près), et donc \(B\) est un multiple (positif, puisque admet des 1 sur la diagonale) du produit scalaire invariant.

Classification

Graphe (semi)-définis positifs

On dit qu’un graphe de Coxeter est défini positif (resp. semi-défini positif) si la matrice de Gram \(A\) associée l’est (ou de façon équivalente, \(2A\)).

On dit qu’un graphe de Coxeter \(\Gamma\) contient un graphe de Coxeter \(\Gamma’\) si \(\Gamma’\) s’obtient à partir de \(\Gamma\) en supprimant des arêtes et/ou en diminuant des poids.
On obtient aussi une relation d’ordre partiel sur les graphes de Coxeter, notée \(\Gamma’ \prec \Gamma\) pour indiquer une inclusion stricte.

Exemple

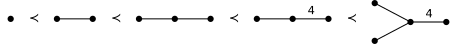
Lemme
Une matrice symétrique est définie positive si et seulement si tous ses mineurs principaux sont strictement positifs.

Variante: si le déterminant est nul est que tous les autres mineurs principaux sont strictement positifs, alors la matrice est semi-définie positive.

Démonstration :
Si \(A\) est symétrique définie positive alors ses valeurs propres sont réelles strictement positives, et donc \(\det A > 0\). De plus la restriction de \(q_A\) à tout sous-espace est encore définie positive, ce qui donne la positivité des mineurs en restreignant au sous-espace engendré par \(e_1, \dots, e_k\) pour chaque \(k\).

La réciproque est claire en dimension 1. Supposons maintenant la réciproque vraie en dimension \(n-1\), et montrons la en dimension \(n\).
Écrivons \({\mathbb R}^n = {\mathbb R}^{n-1} \oplus {\mathbb R}\), alors la restriction de \(q_A\) au facteur \({\mathbb R}^{n-1}\) est définie positive par hypothèse de récurrence.
De plus \(\det A >0\), donc \(q_A\) est non dégénéré, donc \(({\mathbb R}^{n-1})^\perp\) est une droite \(\mathrm{Vect} (e)\), et on a une somme directe orthogonale \({\mathbb R}^n = {\mathbb R}^{n-1} \oplus \mathrm{Vect} (e)\).
Notons \(A’\) la matrice de la restriction de \(q_A\) à \({\mathbb R}^{n-1}\) (dans une base quelconque), alors \(\det A\) et \(\det A’ \cdot q_A(e)\) ont même signe, et donc \(q_A(e) > 0\) et \(A\) est définie positive.

Preuve de la variante :
à nouveau on écrit \({\mathbb R}^n = {\mathbb R}^{n-1} \oplus {\mathbb R}\), et la restriction de \(q_A\) au
facteur \({\mathbb R}^{n-1}\) est définie positive par ce qui précède.
Soit \(e\) un vecteur isotrope pour \(q_A\), alors on a une somme directe orthogonale \({\mathbb R}^n = {\mathbb R}^{n-1} \oplus \mathrm{Vect} (e)\), et \(q_A\) est positive comme somme directe d’une définie positive sur \({\mathbb R}^{n-1}\) et de la forme triviale sur \({\mathbb R}\).

Une matrice est indécomposable si aucune permutation des vecteurs de
la base canonique ne la rend (non trivialement) diagonale par blocs.

Lemme
Soit \(A\) une matrice symétrique semi-définie positive indécomposable, avec tous les coefficients non diagonaux \(a_{ij}\) négatifs ou nuls. Alors le cone isotrope est ou bien réduit à \(\{0\}\), ou bien égal à une droite. De plus la plus petite valeur propre de \(A\) a multiplicité \(1\), et il existe un vecteur propre associé dont toutes les coordonnées sont strictement positives.

Démonstration :
Comme \(A\) est semi-définie le cône isotrope est égal au noyau.
Soit \(x \neq 0\) dans le cône isotrope, et \(z\) le vecteur obtenu en prenant la
valeur absolue des coordonnées de \(x\). L’hypothèse \(a_{ij} \le 0, i\neq j,\)
implique
\[ 0 \le z^t A z \le x^t A x = 0 \]
donc \(z\) est aussi dans le cône isotrope.
Pour tout \(i\), on a \(\sum a_{ij} z_j = 0\).
Soit \(J\) l’ensemble des indices \(j\) avec \(z_j > 0\), et \(I\) son complément, correspondant à l’ensemble des indices \(i\) avec \(z_i = 0\).
On obtient que \(a_{ij} = 0\) pour tout \(i \in I, j \in J\), et donc \(I\) est vide par indécomposabilité de \(A\).
Ainsi le noyau de \(A\) est \(\{0\}\) ou une droite (tout sous-espace de dimension \(\ge 2\) contient un vecteur non nul avec au moins une coordonnée nulle), et la conclusion s’obtient en appliquant ce fait à la matrice symétrique semi-définie positive \(A – \lambda \mathrm{Id}\), avec \(\lambda\) la plus petite valeur propre.

Proposition
Soit \(\Gamma’ \prec \Gamma\) deux graphes de Coxeter distincts.
Si \(\Gamma\) est connexe et semi-défini positif, alors \(\Gamma’\) (qui n’est
pas forcément connexe) est défini positif.

Démonstration :
On numérote les sommets de \(\Gamma’\) de \(1\) à \(k\), puis ceux restant de \(\Gamma\) de \(k+1\) à \(n\).
Soit \(A’\) la matrice de \(\Gamma’\), c’est une matrice \(k \times k\) avec pour tous \(1 \le i,j \le k\)
\[
a_{ij}’ = – \cos \frac{\pi}{m_{ij}’} \ge – \cos \frac{\pi}{m_{ij}} = a_{ij}.
\]
Par l’absurde, supposons que \(x= (x_1, \dots, x_k) \neq 0\) vérifie \(x^t A’ x \le 0\).
Alors en appliquant \(A\) au vecteur \((|x_1|, \dots, |x_k|, 0, \dots, 0)\) on obtient
\[
0 \le \sum a_{ij} |x_i||x_j| \le \sum a_{ij}’ |x_i||x_j| \le \sum a_{ij}’ x_ix_j \le 0.
\]
Donc les inégalités sont des égalités.
Par le lemme, l’égalité \(0 = \sum a_{ij} |x_i||x_j|\) implique \(k = n\), et \(|x_i| > 0\) pour tout \(i\). Alors l’égalité \(\sum a_{ij} |x_i||x_j| = \sum a_{ij}’ |x_i||x_j|\) implique \(a_{ij} = a_{ij}’\) pour tous \(i,j\), contredisant que \(\Gamma’\) est un sous-graphe propre.

Théorème

1. Les graphes de la figure 1 sont la liste complète des graphes de Coxeter connexes défini positifs.
2. En ajoutant les graphes de la figure 2 on obtient la liste complète des graphes de Coxeter connexes semi-défini positifs.

Remarque
Les restrictions sur \(n\) sont pour éviter les redondances. En particulier on a les coïncidences suivantes :
\[\begin{array}{cccccc}
A_2 = I_2(3); &&
B_2 = I_2(4); &&
H_2 = I_2(5); &&
G_2 = I_2(6).
\end{array}\]

Preuve du théorème : cas de 1 ou 2 sommets

Les calculs sont directs. Pour \(\Gamma\) de type \(A_1\), on a \(2A = (2)\) et \(\det \Gamma = 2\). Pour \(\Gamma\) de type \(I_2(m)\) avec \(m \ge 3\), on a
\[\begin{array}{c}
2A =
\begin{pmatrix}
2 & -2\cos \frac{\pi}{m} \\
-2\cos \frac{\pi}{m} & 2
\end{pmatrix},
&&
\det \Gamma = 4\sin^2 \frac{\pi}{m}.
\end{array}\]
On obtient en particulier le tableau de valeurs

m:	3	4	5	6	\(\infty\)
\(\sin \frac{\pi}{m}\):	\(\frac{\sqrt 3}{2}\)	\(\frac{\sqrt 2}{2}\)	–	\(\frac12\)	0
\(\det \Gamma\) :	3	2	\(\frac{5-\sqrt 5}{2}\)	1	0

Remarque
Calcul de \(\cos \frac{\pi}{5}\) et \(\sin^2 \frac{\pi}{5}\).

D’abord
\[\cos 2\theta = {\mathbb R}e (e^{2\theta}) = {\mathbb R}e ((e^\theta)^2) = \cos^2 \theta – \sin^2 \theta = 2\cos^2 \theta -1.\]
Posons \(a = \cos \frac{\pi}{5}\) et \(b = \cos \frac{2\pi}{5}\). Remarquons que \(-a = \cos \frac{4\pi}{5}\), et donc
\[\begin{array}{cc}
b = 2a^2 -1, && -a = 2b^2 -1.
\end{array}\]
Par soustraction, \(a+ b = 2(a+b)(a-b)\), et donc \(a -b = \frac12\).
En remplaçant, on trouve que \(a\) est la racine positive de
\[4a^2 -2a -1 = 0\]
et finalement
\[\begin{array}{cc}
\cos \frac{\pi}{5} = \frac{1+\sqrt 5}{4},
&&
\sin^2 \frac{\pi}{5} = \frac{5-\sqrt 5}{8}.
\end{array}\]

Les graphes de la figure 1 sont définis positifs

Pour chacun des graphes de la figure (sauf \(D_4\), voir plus bas), on peut numéroter les \(n\) sommets de façon à ce que pour chaque \(i = 1, \dots, n\), le sous-graphe \(\Gamma_i\) induit par les \(i\) premiers sommets soit connexe (et donc aussi dans la liste), et que la dernière arête rajoutée soit de poids 3 entre les sommets \(n-1\) et \(n\).
Notons \(d_i = \det \Gamma_i\).
Par hypothèse les \(d_i\) sont les mineurs principaux de la matrice \(2A\), qui est de la forme
\[
2A =
\begin{pmatrix}
* & \dots & * & * & 0 \\
\vdots & \ddots & \vdots & \vdots & \vdots \\
* & \dots & * & * & 0 \\
* & \dots & * & 2 & -1 \\
0 & \dots & 0 & -1 & 2
\end{pmatrix}
\]
En développant suivant la dernière ligne on obtient la relation
\[
d_n = 2d_{n-1} – d_{n-2}.
\]
Par récurrence, on obtient la table suivante qui calcule les déterminants de tous les graphes de la figure (et aussi de \(D_2 = A_1 \times A_1\) qui est non connexe, mais qui avec \(D_3 = A_3\) intervient dans le calcul de \(D_4\)).
En particulier les mineurs \(d_i\) sont tous strictement positifs, et on conclut par le critère de Sylvester.

\(A_n\)	\(B_n\)	\(D_n\)	\(E_6\)	\(E_7\)	\(E_8\)	\(F_4\)	\(H_3\)	\(H_4\)
n+1	2	4	3	2	1	1	\(3 – \sqrt 5\)	\(\frac{7 – 3\sqrt 5}{2}\)

Précisément on utilise les suites suivantes pour \(d_{n-2}, d_{n-1}, d_n\):

• \(A_{n-2} \prec A_{n-1} \prec A_n\) initialisée avec \(\det A_1 = 2\), \(\det
  I_2(3) = 3\);
• \(B_{n-2} \prec B_{n-1} \prec B_n\) initialisée avec \(\det A_1 = 2\), \(\det
  I_2(4) = 2\);
• \(D_{n-2} \prec D_{n-1} \prec D_n\) initialisée avec \(\det A_1 \times A_1 =
  4\), \(\det A_3 = 4\);
• \(A_4 \prec D_5 \prec E_6\);
• \(D_5 \prec E_6 \prec E_7\);
• \(E_6 \prec E_7 \prec E_8\);
• \(A_2 \prec B_3 \prec F_4\);
• \(A_1 \prec I_2(5) \prec H_3\), noter que \(3 – \sqrt 5 \simeq 0.76 > 0\);
• \(I_2(5) \prec H_3 \prec H_4\), noter que \(\frac{7 – 3\sqrt 5}{2} \simeq
  0.15 > 0\).

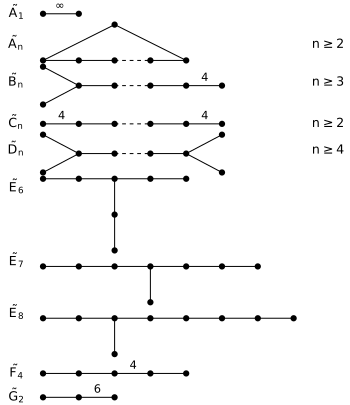
Les graphes de la figure 2 sont semi-définis positifs

Tous d’abord on observe que l’on peut réaliser chacun des graphes \(\Gamma\) comme une suite croissante de graphes connexes dont tous les éléments sauf le dernier sont dans la liste, et tel que la dernière arête ajoutée est de poids \(3\) ou \(4\) entre les sommets \(n-1\) et \(n\). Par la variante du critère de Sylvester, il suffit de montrer que \(\det \Gamma = 0\).

On l’a déjà vu pour \(\tilde A_2\), et pour \(\tilde A_n\), \(n \ge 3\), il suffit de constater que chaque ligne comporte un \(2\), deux \(-1\) et des \(0\), ainsi la somme des colonnes est nulle.

Pour les graphes \(\tilde B_n\) et \(\tilde C_n\), comme précédemment on utilise une relation de récurrence entre les mineurs \(d_{n-2}, d_{n-1}\) et \(d_n\), mais cette fois le poids de la dernière arête ajoutée étant 4 cette relation prend la forme
\[
d_n = 2 (d_{n-1} – d_{n-2}).
\]
obtenue en développant le déterminant de
\[
2A =
\begin{pmatrix}
* & \dots & * & * & 0 \\
\vdots & \ddots & \vdots & \vdots & \vdots \\
* & \dots & * & * & 0 \\
* & \dots & * & 2 & – \sqrt 2 \\
0 & \dots & 0 & -\sqrt 2 & 2
\end{pmatrix}
\]

On trouve \(\det \Gamma = 0\) à l’aide des suites

• \(D_{n-1} \prec D_n \prec \tilde B_n\);
• \(B_{n-1} \prec B_n \prec \tilde C_n\).

Pour les graphes restants, on peut supposer la dernière arête de poids 3 et utiliser la relation de récurrence
\[
d_n = 2 d_{n-1} – d_{n-2}.
\]

Précisément, on peut utiliser les suites

• \(A_1 \times A_1 \times A_1 \prec D_4 \prec \tilde D_4\);
• \(A_1 \times D_{n-2} \prec D_n \prec \tilde D_n\) pour \(n \ge 5\);
• \(A_5 \prec E_6 \prec \tilde E_6\);
• \(D_6 \prec E_7 \prec \tilde E_7\);
• \(E_7 \prec E_8 \prec \tilde E_8\);
• \(A_3 \prec B_4 \prec \tilde F_4\);
• \(A_1 \prec G_2 \prec \tilde G_2\).

Figure 1 : graphes de Coxeter définis positifs

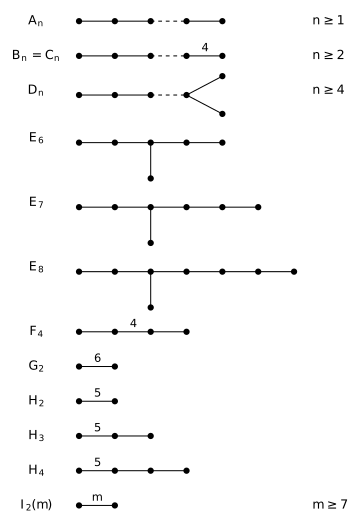
Figure 2 : graphes de Coxeter semi-définis positifs

Tout graphe semi-défini positif est dans une des deux listes

Supposons que \(\Gamma\) est un graphe connexe semi-défini positif à \(n\) sommets
et poids maximal \(m\), qui n’apparaisse pas dans une des deux listes.

1. Le nombre \(n\) de sommets est au moins 3, puisqu’on a traité exhaustivement
   les cas de 1 ou 2 sommets.
2. \(m\) est fini et \(m \le 5\), puisque \(\Gamma\) ne contient pas le graphe
   \(\tilde A_1\) ni le graphe \(\tilde G_2\).
3. Le cas \(m = 5\) est impossible, car \(\Gamma\) ne contenant pas \(\tilde B_n\)
   n’admet donc pas de point de branchement, et les deux graphes
   • >\(Z_4 =\)
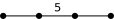
   • >\(Z_5 =\)

   sont de déterminant \(<0\), ce que l'on voit par exemple en appliquant la formule
   \[
   d_n = 2 d_{n-1} – d_{n-2}.
   \]
   aux suites

   • \(A_2 \to H_3 \to Z_4\);
   • \(H_3 \to H_4 \to Z_5\).
4. Supposons maintenant \(m =4\).
   \(\Gamma\) ne contient pas \(\tilde C_n\), donc une seule arête admet le poids \(4\),
   et comme il ne contient pas \(\tilde B_n\), il n’a pas de point de branchement.
   Les deux arêtes extrèmes sont de poids 3, sinon \(\Gamma = B_n\).
   Comme \(\Gamma \neq F_4\) et \(\Gamma\) ne contient pas \(\tilde F_4\), cela épuise
   toutes les possibilités avec \(m = 4\).
5. Finalement supposons \(m=3\).
   \(\Gamma\) doit admettre un point de branchement, sinon \(\Gamma = A_n\).
   \(\Gamma\) ne contient pas \(\tilde D_4\), donc admet seulement des point de
   branchement triples.
   \(\Gamma\) ne contient pas \(\tilde D_n\), donc admet exactement un point de
   branchement triple, avec branche de longueur \(2 \le a \le b \le c\).
   \(\Gamma\) ne contient pas \(\tilde E_6\), donc \(a = 2\).
   Comme \(\Gamma \neq D_n\), on a \(b \ge 3\), mais comme \(\Gamma\) ne contient pas
   \(\tilde E_7\), on a \(b = 3\).
   Finalement \(3 \le c \le 5\) puisque \(\Gamma\) ne contient pas \(\tilde E_8\), mais
   les cas \(c = 3, 4 , 5\) correspondraient à \(\Gamma = E_6, E_7, E_8\), ce qui est
   exclu.

Réalisation

Groupes de réflexions finis

Soit \(V\) un espace vectoriel euclidien, \(H \subset V\) un hyperplan, \(\alpha \in V\) un vecteur.
On note \(s_H\) la réflexion orthogonale associé à \(H\), et \(s_\alpha\) la réflexion orthogonale associée à \(\alpha^\perp\).
Explicitement:
\[
s_\alpha(x) = x – 2\frac{\langle \alpha,x \rangle}{\langle \alpha, \alpha \rangle} \alpha.
\]

Un groupe de réflexions fini est un groupe fini \(W \subset \mathrm O(V)\) engendré par des réflexions orthogonales.
Le groupe \(W\) est dit essentiel si l’origine est le seul point fixe (ou autrement dit, \(\bigcap_{s_H \in W} H = \{ 0 \}\)).

Un ensemble de vecteur \(\Phi = \{\alpha\}\) est un système de racine (généralisé) si les réflexions \(s_\alpha\), \(\alpha \in \Phi\) engendre un groupe fini \(W\), et que \(\Phi\) est invariant par \(W\).

On suppose toujours un tel système de racine réduit, au sens où \(\alpha, \beta \in \Phi\) colinéaires implique \(\alpha = \pm \beta\).

Un système de racine est dit cristallographique si pour tout \(\alpha, \beta \in \Phi\), le coefficient \(2\frac{\langle \alpha,x \rangle}{\langle \alpha, \alpha \rangle}\) est entier.
Cela implique que le groupe additif engendré par \(\Phi\) est un réseau de \(V\).

On donne des réalisations combinatoires et/ou géométriques des groupes de Coxeter des diagrammes du tableau.

• \(A_n\) correspond au groupe symétrique, pour le système de générateurs \((i \, i+1)\).
  Géométriquement, c’est le groupe des isométries préservant un simplexe régulier dans l’espace euclidien de dimension \(n\).

• \(B_n\) correspond au groupe des permutations signées, pour le système de générateurs \((i \, i+1)\) plus le « flip » de \(n\).
  Géométriquement, c’est le groupe des isométries préservant un hypercube dans l’espace euclidien de dimension \(n\) (\(n\) paires de faces opposées).

• \(D_n\) est le groupe des permutations signées avec un nombre pair de \(-\).
  Géométriquement, c’est le groupe des isométries préservant un demi-hypercube dans l’espace euclidien de dimension \(n\)

• \(H_3\) est le groupe de l’icosaèdre (ou dodécaèdre), \(H_4\) le groupe du \(120\)-cellules (ou \(600\)-cellules), et \(F_4\) le groupe du \(24\)-cellules.

Complexes de coxeter

Groupe de réflexion fini

Soit \(W\) un groupe de réflexions fini, c’est à dire \(W \subseteq \mathrm O_n({\mathbb R})\) est
un sous-groupe fini du groupe orthogonal standard engendré par des réflexions
orthogonales.
On suppose \(W\) irréductible (pas de sous-espace propre invariant) et essentiel
(pas de point fixe global à part l’origine).
Soit \(H_i\) l’ensemble des hyperplans correspondant à des réflexions
orthogonales \(s_i \in W\) (pas seulement les générateurs), et \(\ell_i\) des
formes linéaires définissant les \(H_i\).
On appelle chambre une composante connexe de \({\mathbb R}^n \setminus \bigcup H_i\).
En particulier le choix des \(\ell_i\) conduit à un choix de chambre fondamentale
\[
C = \{ v \in {\mathbb R}^n \mid \ell_i(v) > 0 \text{ pour tout } i\}
\]
Deux chambres qui ont une face de codimension 1 commune (correspondant à traverser l’un des \(H_i\)) sont dites adjacentes.
Une suite de chambres \((C_j)_{0\le j \le r}\) est une gallerie de longueur \(r\) si \(C_j\) est adjacente à \(C_{j+1}\) pour tout \(j\).
La gallerie est dite minimale s’il n’y a pas de gallerie de longueur \(< r\) entre \(C_0\) et \(C_r\).
Le fait suivant me semble géométriquement clair:

Deux chambres sont toujours connectées par au moins une gallerie, et une gallerie est minimale si et seulement si elle ne traverse aucun hyperplan plus d’une fois.

Le lemme suivant semble être implicite dans \cite[p. 36]{AB}:

Lemme
Le groupe \(W\) agit transitivement sur les chambres.

Démonstration :
Le fait qu’il existe une action est claire, il s’agit de montrer que toute chambre \(D\) est dans l’orbite de la chambre fondamentale \(C\).
On procède par récurrence sur la distance \(r\) entre \(C\) et \(D\) (\(r\) est le
nombre d’hyperplans séparant ces deux chambres).
Si \(r = 1\), on envoie \(D\) sur \(C\) par la réflexion d’hyperplan séparant \(D\) et \(C\).
Si \(r > 1\), on considère une gallerie \(C_0 = C, C_1, \dots, C_r = D\), on prend
\(s_1\) la réflexion échangeant \(C\) et \(C_1\), et on applique l’hypothèse de
récurrence à \(C = s_1 C_1\) et \(s_1 D\).

Proposition
Soit \(\{H_s\}\) l’ensemble des hyperplans d’appui de \(C\), \(S\)
l’ensemble des réflexions orthogonales \(s \in W\) associées, et \(e_s\) le vecteur
unitaire normal à \(H_s\) et pointant vers le demi-espace contenant \(C\).
Alors:

1. Pour chaque \(s,t \in S\), on a \(\langle e_s, e_t \rangle = – \cos \frac{\pi}{m(s,t)} \le 0\) où
   \(m(s,t)\ge2\) est l’ordre de \(st\).
2. La chambre \(C\) est simpliciale, ce qui revient à dire que \(S\) est de cardinal
   \(n\);
3. \(S\) engendre \(W\);
4. \(\bar C\) est un domaine fondamental pour l’action de \(W\) sur
   \({\mathbb R}^n\);
5. \(W\) agit simplement transitivement sur les chambres.

Démonstration :
1. C’est juste la remarque que le groupe \(\langle s,t \rangle\) agissant sur \((H_s \cap
H_t)^\perp = {\mathbb R} e_s \oplus
{\mathbb R} e_t\) est le groupe diédral d’ordre \(m(s,t)\).

2. L’ensemble des hyperplans d’appui est de cardinal \(r \ge n\) sinon l’action neserait pas essentielle. Par l’absurde supposons \(r > n\). Donc les \(\ell_s = \langle e_s, \cdot \rangle\) forment une famille liée, et il existe une relation linéaire nulle non-triviale dont tous les coefficients sont positifs (sinon on écrit une égalité entre combinaisons linéaires non nulles à coefficients positifs, et comme les coefficients non diagonaux sont \(\le 0\), le produit scalaire est \(\le 0\), mais aussi \(\ge 0\) puisque c’est le produit scalaire d’un vecteur avec lui-même, donc \( =0\), absurde). Une telle combinaison est incompatible avec la définition de \(C\) comme quadrant positif.

3. Dans le lemme on a en fait montré que le groupe \(\langle S \rangle\) agit transitivement sur les chambres. Toute réflexion \(s_i\) dans \(W\) correspondant à un mur d’au moins une chambre \(D\), en utilisant le fait qu’il existe \(w \in \langle S \rangle\) tel que \(w D = C\), on obtient \(w s_i w^{-1} \in S\), et donc également \(s_i \in \langle S \rangle\). Comme les \(s_i\) engendrent \(W\), on obtient \(W = \langle S \rangle\).

4. Soit \(w \in W\) et \(x,y \in \bar C\) tel que \(wx = y\). On veut montrer \(x = y\). On écrit \(w = s_1 \dots s_r\) sous forme réduite, et on procède par récurrence sur la longueur \(r\) de \(w\). Si \(r = 0\), \(w = \mathrm{Id}\) et c’est fini. Sinon, on remarque que \(wC\) et \(C\) sont de part et d’autre de l’hyperplan
\(H_{s_1}\) (par minimalité de \(r\), et par la propriété « deletion » qui est assez claire géométriquement). Donc \(wx = y \in H_{s_1}\). Mais alors en appliquant \(s_1\) on trouve \(s_2 \dots s_r x = s_1 y = y\), et on conclut par hypothèse de récurrence.

5. Juste la remarque que dans la preuve précédente, si \(x = y \in C\), alors le seul \(w \in W\) fixant \(x\) est l’identité.

La décomposition simpliciale de la sphère \(S^{n-1} \subset {\mathbb R}^n\) est appelée le complexe de Coxeter (« sphérique ») associé au groupe de réflexion fini \(W\).

Une autre propriété importante est le

Théorème
Avec les notations de la proposition, \((W,S)\) est un système de Coxeter.

La preuve, combinatoire, est liée au problème du mot, est ne semble pas plus facile dans le cas fini que dans le cas général.