On utilise librement les notations et définitions des exposés sur les algèbres de Lie (ici). Tout au long de ces notes \( F \) est un corps de caractéristique 0 et \( \mathfrak{g} \) une algèbre de Lie semisimple sur \( F \).

Groupes de Coxeter sphériques associés aux algèbres de Lie

Algèbres semisimples déployées

Soient \( F \) un corps de caractéristique 0 et \( \mathfrak{g} \) une algèbre de Lie semisimple sur \( F \). Soit \( E \) la clotûre algébrique de \( F \) ; on sit que \( \mathfrak{g} \) est déployée sur \( F \) s’il existe une sous-algèbre de Cartan \( H \) de \( \mathfrak{g} \otimes_F E \) telle que \( \dim_F(H \cap \mathfrak{g}) = \dim_E(H) \) et pour tout \( x \in H \cap \mathfrak{g} \) on a que \( \mathrm{ad}_x \) est diagonalisable sur \( F \). On peut alors appliquer la théorie vue dans le cas algébriquement clos à \( \mathfrak{g} \) sur \( F \) et on obtient le résultat suivant.

Théorème : Soit \( g \) une algèbre de Lie semisimple déployée sur \( F \). Soit \( H \) une sous-algèbre de Cartan de \( \mathfrak{g} \) et \( H^* \) son dual. Il existe un sous-ensemble \( \Phi = \Phi(\mathfrak{g}, H) \) de \( H^* \) tel que l’on ait la décomposition
\[
\mathfrak{g} = H \oplus \bigoplus_{\alpha \in \Phi} \mathfrak{g}_\alpha, \: \mathfrak{g}_\alpha = \{ x \in \mathfrak{g} : \forall h \in H, \mathrm{ad}_h(x) = \alpha(h)x \}.
\]

Groupe de Coxeter d’un système de racines

Si \( h \in H \) on a d’après la décomposition radicielle \( \mathrm{tr}(\mathrm{ad}_h) = \sum_{\alpha \in \Phi} \alpha(h)^2 \). En particulier, si \( F = {\mathbb R} \) la forme de Killing est définie positive en restriction à \( H \).

En général, pour définir un espace euclidien associé à \( \mathfrak{g} \) (et au choix de la sous-algèbre de Cartan) on utilise le lemme suivant.

Lemme : On peut choisir des générateurs \( X_\alpha \) des \( \mathfrak{g}_\alpha \) et \( H_1, \ldots, H_r \) de \( H \) tels que les crochets de Lie \( [X_\alpha, X_\beta] \) et \( [X_\alpha, H_i] \) soient des \( {\mathbb Q} \)-combinaisons linéaires des \( X_\alpha, H_i \).

La démonstration utilise la théorie des \( \mathfrak{sl}_2 \)-triplets et est donc un peu longue pour être donnée ici. On peut ausi déduire le lemme a posteriori de la classification des algèbres de Lie semsisimples scindées : il se trouve qu’elles sont toutes définissables sur \( {\mathbb Q} \).

Il suit du lemme que si on définit \( \mathfrak{g}_{\mathbb Q} \) comme le \( {\mathbb Q} \)-sous-espace de \( \mathfrak{g} \) engendré par les \( X_\alpha, H_i \) alors c’est une \( {\mathbb Q} \)-sous algèbre de Lie de \( \mathfrak{g} \) et on a \( \mathfrak{g} = F \otimes_{\mathbb Q} \mathfrak{g}_{\mathbb Q} \). La forme quadratique induite sur \( H_{\mathbb Q} \otimes_{\mathbb Q} {\mathbb R} \) par la forme de Killing \( K \) est alors définie positive. On définit alors l’espace euclidien \( V \) comme l’espace dual \( H_{\mathbb Q}^* \otimes_{\mathbb Q} {\mathbb R} \) munie de la forme duale de \( K \).

Il suit du lemme que \( \Phi \subset H_{\mathbb Q}^* \). La démonstration du lemme ci-dessus montre en fait que \( \Phi \) est un système de racines au sens axiomatique (cf. Bourbaki). La seule conséquence qui nous intéresse ici est la suivante.

Lemme : Soit \( \alpha \in \Phi \) et \( s_\alpha \) la réflexion orthogonale de \( V \) de miroir l’orthogonal de \( \alpha \). On a \( s_\alpha\Phi = \Phi \).

Soit \( W \) le sous-groupe de \( \mathrm O(V) \) engendré par les réflexions \( s_\alpha \). Par la théorie générale exposée dans les notes de Stéphane il existe un sous-ensemble \( \Delta \subset \Phi \) ayant les propriétés suivantes :

1. \( \Delta \) est une base de \( H^* \) ;
2. Si \( \alpha \in \Phi \) elle s’écrit sous la forme \( \pm \sum_{\beta \in \Delta} n_\beta \beta \) pour des \( n_\beta \in \mathbb N \) ;
3. \( (W, s_\beta) \) est un groupe de Coxeter.

Un tel \( \Delta \) est appelé une base du système de racines \( \Phi \). On notera \( \Phi^+ \) l’ensemble des racines positives pour \( \Delta \), c’est-à-dire qui s’écrivent \( \sum_{\beta \in \Delta} n_\beta \beta \), \( n_\beta \mathfrak{g}e 0 \).

Exemple : \( \mathfrak{g} = \mathfrak{sl}_3(F) \)

Dans ce cas on prend comme sous-algèbre de Cartan :
\[
H = \left\{ \begin{pmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \end{pmatrix} : a, b, c \in F, a + b + c = 0 \right\}.
\]
et on note \( L_i \) la forme linéaire sur \( \mathfrak{gl}_3(F) \) défine par \( L_i(a_{ij}) = a_{ii} \). Alors \( \Phi = \{ \alpha_{ij} = L_i – L_j : i\not= j \} \) est le système de racines de \( \mathfrak{sl}_3 \) : le sous-espace \( (\mathfrak{sl}_3)_{\alpha_{ij}} \) est donné par les matrices \( (a_{kl}) \) avec \( a_{kl} = 0 \) si \( (k, l) \not= (i, j) \).

Une base de \( \Phi \) est donnée par exemple par \( \{L_1 – L_2, L_2 – L_3\} \). Le groupe de Coxeter est de type \( \mathrm A_3 \), en particulier isomorphe au groupe symétrique \( S_3 \).

Appartement d’un groupe algébrique semisimple

Soit \( \mathbf{G} \) un groupe algébrique connexe sur \( F \) dont l’algèbre de Lie est \( \mathfrak{g} \). Il existe un unique sous-\( F \)-groupe connexe \( \mathbf T \le \mathbf G \) tangent à \( H \). On note \( X(\mathbf T) = \hom_F(\mathbf T, F^\times) \) le groupe des caractères de \( \mathbf T \), qui est un groupe abélien libre de rang \( \dim(\mathbf T) \). On note \( \mathbf N = N_{\mathbf G}(\mathbf T) \) le normalisateur dans \( \mathbf{G} \) de \( \mathbf T \) (qui est un \( F \)-sous-groupe) ; on remarque que comme \( \mathbf{G} \) est connexe \( \mathbf T \) est égal à son propre centralisateur.

Lemme : On a des isomorphismes naturels \( e : V \cong X^*(\mathbf T) \otimes_{\mathbb Z} {\mathbb R}\) et \( f : W \cong \mathbf N(F)/\mathbf T(F) \). De plus \( e(w\xi) = f(w)e(\xi) \) pour touts \( \xi \in V \) et \( w \in W \).

BN-paires et construction de l’immeuble

Sous-groupe de Borel

Soit \( \mathfrak{n} = \bigoplus_{\alpha \in \Phi^+} \mathfrak{g}_\alpha \). Alors \( \mathfrak{n} \) est une sous-algèbre de Lie de \( \mathfrak{g} \) d’après la règle \( [\mathfrak{g}_\alpha, \mathfrak{g}_\beta] \subset \mathfrak{g}_{_alpha+\beta} \), puisque \( \Phi^+ \) est stable par addition. Il existe un unique sous-\( F \)-groupe connexe \( \mathbf U \le \mathbf{G} \) tangent à \( \mathfrak{n} \), et comme \( \mathfrak{n} \) est normalisée par \( H \), le sous-groupe \( \mathbf B = \mathbf T\mathbf U \) est le sous-\( F \)-groupe connexe tangent à \( H + \mathfrak{n} \). On l’appelle sous-groupe de Borel de \( \mathbf G \).

On peut montrer « à la main » qu’il existe un immeuble \( X \) dont les appartements sont des complexes de Coxeter pour \( V \) et sur lequel \( \mathbf G(F) \) agit en prolongeant l’action de \( \mathbf N(F) \) sur \( V \). Les chambres de cet immeuble sont en bijection avec l’ensemble \( \mathbf G(F) / \mathbf B(F) \), sur lequel on peut construire une relation d’adjacence ad hoc. Dans la suite on va plutôt expliquer une machinerie formalisant cette construction purement en termes de théorie des groupes.

BN-paires

Définition : Soit \( G \) un groupe et \( B, N \) des sous-groupes de \( G \) ; on note \( T = N \cap B \), on suppose que \( T \triangleleft N \) et on pose \( W = N/T \). On dit alors que \( (B, N) \) est une BN-paire si \( G = \langle B, N \rangle \), et il existe une famille génératrice \( S \) de \( W \) vérifiant les deux conditions suivantes :

1. Pour touts \( s \in S, w \in W \) on a \( sBw \subset BwB \cup BswB \) ;
2. Pour tout \( s \in S \) on a \( sBs^{-1} \not\subset B \).

Il suit de cette définition que \( (W, S) \) est un groupe de Coxeter (cf. Abramenko–Brown, Proposition 6.40) ; dans les cadres où on l’appliquera ceci sera déjà connu. Le lien avec les immeubles est donné par le résultat suivant (loc. cit., Theorem 6.56).

Théorème : Avec les notations ci-dessus il existe un immeuble épais dont les appartements sont isomorphes au complexe de Coxeter de \( (W, S) \), l’ensemble des chambres est \( G/B \) et les appartements sont les orbites des classes à gauche \( gT, g \in G \) sur cet ensemble. En particulier \( G \) agit par automorphismes sur cet immeuble, et l’action est transitive sur les chambres.

Les stabilisateurs des simplexes de l’immeuble sont les sous-groupes paraboliques de \( G \) associés à la BN-paire. Pour les décrire on commence par définir un sous-groupe parabolique standard comme suit : c’est un sous-groupe de la forme \( \langle T, B \rangle \) où \( T \subset S \). Ces derniers sont les stabilisateurs des faces de la chambre fondamentale (correspondant à la classe triviale \( 1B \in G/B) \). Un sous-groupe est donc parabolique s’il est conjugué par un élément de \( G \) à un sous-groupe parabolique standard.

BN-paire d’un groupe algébrique

L’ingrédient qui nous manque encore pour la construction de l’immeuble d’un \( F \)-groupe déployé \( \mathbf G \) est le suivant.

Lemme : Si \( \mathbf N, \mathbf B \) sont les \( F \)-sous-groupes de \( \mathbf G \) définis plus haut alors \( (\mathbf B(F), \mathbf N(F)) \) est une BN-paire.

De plus le groupe de Coxeter associé est bien le groupe de Weyl \( W = \mathbf N(F) / \mathbf T(F) \). On a donc bien un immeuble dont les appartements sont \( V \) et sur lequel \( \mathbf G(F) \) agit.

Dans ce cadre la définition ci-dessus de sous-groupe parabolique standard correspond à la définition classique : ce sont les groupes \( \mathbf P(F) \) où \( \mathbf B \le \mathbf P \le \mathbf G \) est un \( F \)-sous-groupe. Ils sont en bijection avec les sous-ensembles de la base \( \Delta \) ; si \( \Theta \subset \Delta \) le sous-groupe associé est tangent à la sous-algèbre
\[
H \oplus \mathfrak{n} \oplus \bigoplus_{\theta \in \Theta} \mathfrak{g}_{-\theta}.
\]

Exemple : \( \mathrm{SL}_3 \)

Si \( \mathbf G = \mathrm{SL}_3 \) son algèbre de Lie est \( \mathfrak{sl}_3 \). On a alors
\[
\mathbf T(F) = \left\{ \begin{pmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \end{pmatrix} : abc = 1 \right\}, \, \mathbf B(F) = \left\{ \begin{pmatrix} a & x & y \\ 0 & b & z \\ 0 & 0 & c \end{pmatrix} : abc = 1 \right\}
\]
et \( W \) est le sous-groupe des matrices de permutation. Les sous-groupes paraboliques standard sont \( \mathbf G, \mathbf B \) et les conjugués de
\[
\mathbf P(F) = \left\{ \begin{pmatrix} a & b & x \\ c & d & y \\ 0 & 0 & e \end{pmatrix} : (ad – bc)e = 1 \right\}
\]
(qui correspond à la racine \( L_1 – L_2 \)).

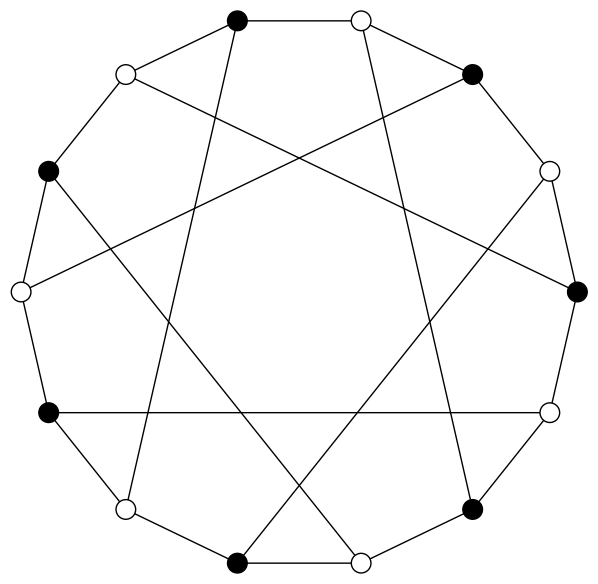
On peut donner dans ce cas une interprétation géométrique de l’immeuble \( I \) associé à \( \mathbf G(F) \) : \( \mathbf G(F)/\mathbf B(F) \) est l’ensemble des drapeaux de \( F^3 \), qui représentent donc les 1-simplexes de \( I \). Les sommets adjacents à un drapeau \( 0 \subset D \subset P \subset F^3 \) sont la droite \( D \) et le plan \( P \) ; deux chambres sont donc adjacentes si elles sont représentées par des drapeaux ayant une droite ou un plan en commun.

Cet immeuble est donc un graphe, de valence \( |F| + 1 \) (le cardinal de la droite projective sur \( F \). Dans le cas où \( F = \mathbb F_2 \) (a priori non traité par les arguments ci-dessus, mais on peut les adapter) il est représenté par l’image suivante.