Examples of 3–manifolds

1. Let \( K \subset \mathbb S^3\) be a knot, and \( \nu K \) a tubular neigbourhood. Then the knot complement \( \mathbb S^3 \setminus \nu K \) is a compact three-manifold with boundary a torus.

   Examples of knots are :

   • The unknot;
   • The trefoil :
     
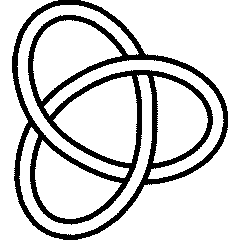
   • The figure-eight :
     
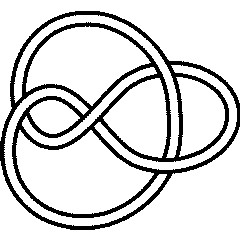
   • The torus knot 5₁ with five crossings, corresponding to the curve of slope (3/2):
     
   • The knot 5₂:
     

   If \( K \) is a knot then we can form its Whitehead double, which is obtianed by embedding in the tubular neighbourhood \( \nu K \) the following knot in the solid torus:
   

2. Let \( \Sigma \) be a compact surface and \( f \in \mathrm{Homeo}^+(\Sigma) \). Then we can form the mapping torus:
   \[
   M = (\Sigma \times [0, 1]) / ((x, 0) = (f(x), 1))
   \]
   which is a compact 3–manifold (whose boundary is composed of as many tori as there are orbits of \( f \) on the components of \( \partial \Sigma \)).
3. A particularly simple case of the construction above is the product \( \Sigma \times \mathbb S^1 \) (corresponding to \( f = \mathrm{Id} \)).
4. If \( M, N \) are two compact manifolds and \( \partial_1 M, \partial_1 N \) are two homeomorphic subsurfaces in the boundaries \( \partial M, \partial N \) then we can glue \( M, N \) along \( \partial_1 M, \partial_1 N \) to get a new compact manifold.
5. A Seifert manifold is a singular \( \mathbb S^1 \)-bundle over a surface. Examples are:
   • The Hopf fibration of \( \mathbb S^3 \) over \( \mathbb S^2 \) shows that \( \mathbb S^3 \) is Seifert;
   • If \( K \) is the trefoil knot, its complement \( \mathbb S^3 \setminus \nu K \) is Seifert fibered. More generally this is true for all torus knot: such a knot lies onto a torus in the Hopf fibration, and by extending the foliation of this torus induced by the knot we obtained a decomposition of \( \mathbb S^3 \) into circles parallel to the knot.

Questions about knots and 3–manifolds

1. Distinguishing knots
2. If \( K \subset \mathbb S^3 \) is a knot there exists an embedded surface \( \Sigma \subset \mathbb S^3 \) such that \( \partial \Sigma = K \), which is often called a Seifert surface. For example here are such surfaces for the trefoil, the figure-eight and 5₁ (source: http://www.win.tue.nl/~vanwijk/seifertview/knot_gallery.htm):
   
   
   

   What is the minimal genus of such a surface? This is denoted by \( g(K) \) and usually called the genus of the knot. For example, the genus of the trefoil is equal to 1 (the surface picyured above is of genus 1, and only the unknot can have genus 0), and the knot 5₁ is of genus at most 2 (realised by the surface pictured above).

3. When is a knot exterior a fibered manifold (as defined above)? It can be shown that this is the case for the trefoil and the figure-eight.
4. Computing the Thurston norm on the first cohomology \( H^1 \) of a three-manifold (in the knot case this is the genus).
5. Which knots are slice, i.e. bound an embedded smooth disc in the four-ball?

Alexander polynomial and Reidemeister torsion

Alexander polynomial of knots

Let \( K \subset \mathbb S^3 \) be a knot and \( X_K = \mathbb S^3 \setminus \nu K \) its exterior. Then \( H^1(X_K) = \langle t \rangle \cong \mathbb Z \) (where \( t \) is a class dual to a Seifert surface) is not useful to distinguish between knots.

On the other hand this makes the ring \( \mathbb Z[t, t^{-1}] \) into a \( \pi_1(X_K) \)-module, and the twisted homology group \( H_1(X_K ; \mathbb Z[t, t^{-1}]) \) (the homology of the unique infinite cyclic covering of \( X_K \)) is much more interesting.

One invariant that it produces is the Alexander polynomial. We will define it in greater generality later, here we will only explain a special case. Suppose that \( H_1(X_K ; \mathbb Z[t, t^{-1}]) \cong \bigoplus_{j=1}^r \mathbb Z[t, t^{-1}] / (p_j(t)) \) as a \( \mathbb Z[t, t^{-1}] \)-module (this is not always the case since \( \mathbb Z[t, t^{-1}] \) is not a principal ring). Then the Alexander polynomial is defined by \( \Delta_K(t) = \prod_j p_j(t) \).

Reidemeister torsion

In this paragraph we will work in a general setting. Let \( X \) be a CW-complex and \( Y \subset X \) a subcomplex. Fix an homomorphism \( \gamma: \pi_1(X) \to {\mathbb Z} \), which we will consider as giving an action of \( pi_1(X) \) on the ring \( {\mathbb Z}[t, t^{-1}] \). Then the Reidemeister torsion of the triple \( (X, Y ; \gamma) \) is an invariant obtained from the twisted chain complex \( C_*(X, Y ; {\mathbb Z}[t, t^{-1}]) \) which lives in the ring \( {\mathbb Z}[t, t^{-1}] \) and is well-defined up to multiplication by a unit (of the form \( \pm t^m \)). It has the following properties:

1. \( \tau(X, Y ; \gamma) = 0 \) if and only if \( H_*(X, Y ; {\mathbb Q}(t)) = 0 \).
2. If the chain complex is concentrated in degrees \( n, n-1 \), i.e. it has the form:
   \[
   C_*(X, Y ; {\mathbb Z}[t, t^{-1}]) \cong 0 \to {\mathbb Z}[t, t^{-1}]^n \overset{A}{\to} {\mathbb Z}[t, t^{-1}]^m \to 0
   \]
   for some \( A \in M_{m\times n}({\mathbb Z}[t, t^{-1}]) \) then \( \tau(X, Y ; \gamma) = \det(A)^{(-1)^n} \).
3. If all chain complexes are acyclic then we have the multiplication formula:
   \[
   \tau(X; \gamma) = \tau(X, Y; \gamma) \cdot \tau(Y; \gamma|_{\pi_1(Y)}).
   \]
4. \( \tau \) is an homology invariant (more general Reidemeister torsions are not, but with coefficients in the abelian group ring \( {\mathbb Z}[t, t^{-1}] \) it’s OK).

Examples:

1. \( \tau(\mathbb S^1 ; \mathrm{Id}) = (1-t)^{-1} \);
2. Let \( \gamma : \pi_1(\Sigma \times \mathbb S^1) \to \pi_1(\mathbb S^1) \) be the natural morphism; then \( \tau(\Sigma \times \mathbb S^1 ; \gamma) = (1-t)^{-\chi(\Sigma)} \);
3. Let \( N \) be the fibered manifold with fiber \( \Sigma \) and monodromy \( f \). Suppose that \( \Sigma \) is noncompact, so that it retracts onto the graph with one vertex and loops \(c_1, \ldots, c_r, \, r = 1-\chi(\sigma) \). Then the chain complex of the infinite cyclic cover is :
   \[
   0 \to \sum_{j=1}^r {\mathbb Z}[t, t^{-1}](c_i \times [0,1]) \overset{(1 – tf_*, 0)}{\to} \left( \sum_{j=1}^r {\mathbb Z}[t, t^{-1}]c_i \right) \oplus {\mathbb Z}[t, t^{-1}] \overset{(0,1 – t)}{\to} {\mathbb Z}[t, t^{-1}] \to 0
   \]
   and it follows that the torsion is given by:
   \[
   \tau(N ; \gamma) = \frac{\det(1 – tf_*)} {1-t}.
   \]
   In particular, the numerator of the Reidemeister torsion of a fibered 3–manifold is always monic.
4. In our examples of knot complements we have:
   1. for the unknot: \( \tau(X_K ; \gamma) = (1-t)^{-1}\);
   2. for the trefoil: \( \tau(X_K ; \gamma) = (1-t)^{-1}(1-t+t^2) \);
   3. for the figure-eight: \( \tau(X_K ; \gamma) = (1-t)^{-1}(1-3t+t^2) \);
   4. for 5₁: \( \tau(X_K ; \gamma) = (1-t)^{-1}(1-t+t^2-t^3+t^4) \);
   5. for 5₂: \( \tau(X_K ; \gamma) = (1-t)^{-1}(2-3t-2t^2) \). Note that this is not monic, hence in this case \( X_K \) is not fibered.
   6. The Reidemeister torsion of any Whitehead double is always equal to \( (1-t)^{-1} \). In particular, the Alexander invariant is not sufficient to detect the unknot.

Further properties of the Reidemeister torsion

1. For knot complements we have \( \tau(X_K; \gamma) = (1-t)^{-1}\Delta_K(t) \).
2. Let \( N \) be a three-manifold and suppose that the Poincaré dual of \( \gamma \in H^1(N) \) is represented in \( H_2(N, \partial N) \) by a surface of genus \( g \ge 1 \). Then the degree of the Reidemeister torsion (the degree of a Laurent polynomial in \( {\mathbb Z}[t, t^{-1}] \) is the difference between the higher and lower powers of \( t \), and the degree of Reidemeister torsion is the difference between that of its numerator and of its denominator) satisfies:
   \[
   \deg(\tau(N, \gamma)) \le 2g – 2.
   \]
   In particular, we get for knots that:
   \[
   \deg(\Delta_K) -1 \le 2g(K) – 1.
   \]
   This show for example that the genus of 5₁ is actually equal to 2 since in this case \( \deg(\Delta_K) = 2 \).
3. Let \( f \mapsto \overline f \) be the involution on \( {\mathbb Z}[t, t^{-1}] \) defined by \( \bar t = t^{-1} \). If \( X \) is a k-dimensional manifold then we have:
   \[
   \tau(X, \gamma) = \overline{\tau(X, \partial X ; \gamma)}^{(-1)^{k+1}}
   \]
   as a consequence of Poincaré duality.
4. If N is a Seifert manifold then \( \tau(N ; \gamma) \) is a product of cyclotomic polynomials for any \( gamma \) (this shows that the figure-eight and 5₂ are not Seifert; in fact they are hyperbolic, as can be deduced from Geometrisation or by directly solving Thurston’s equations).

Reidemeister torsion and slice knots

Theorem (Fox, Milnor): Suppose that \( K \) is a slice knot. Then there exists \( f \in {\mathbb Z}[t, t^{-1}] \) such that
\[
\tau(X_K ; \gamma) = (1-t)^{-1} f(t) f(t^{-1}).
\]

For the proof let \( N_K \) be the result of 0-framed surgery on \( X_K \) (gluing a solid torus \( T \) along a longitude) so that \( \gamma \) factors through \(p_1(N_K) \). Then by the multiplicativity of Reidemeister torsion we get:
\[
\tau(N_K, \gamma) = \tau(T) \tau(X_K) = (1-t)^{-1} \tau(X_K).
\]
Let \( D \) be the disc in \( \mathbb B^4 \) which \( K \) bounds and let \( W = \mathbb B^4 \setminus \nu D \). It is easy to see that \( \partial W \cong N_K \) and that \( \gamma \) extends to an homomorphism \( \pi_1(W) \to {\mathbb Z} \). By Poincaré duality and multiplicativity we get:
\[
\tau(W ; \gamma)^{-1} = \overline{\tau(W, \partial W ; \gamma)} = \overline{\tau(W)}\tau(N_K)^{-1}
\]
so that in fine \( \tau(N_K) = \tau(W) \overline{\tau(W)} \), which finishes the proof.