Rank gradient

For any finitely generated group \( H \) let \( d(H) \) be its rank, the minimal number of elements needed to generate \( H \). If \( H \) is a finite-index subgroup in a finitely generated group \( \Gamma \) then we have
\[
d(H) \le |\Gamma / H| (d(\Gamma) – 1)
\]
and it is thus natural to define:
\[
r(\Gamma, H) = \frac{d(H) – 1}{|\Gamma / H|}.
\]
If \( \Gamma = \Gamma_0 \supset \Gamma_1 \supset \cdots \) is a chain of finite index subgroup then the limit:
\[
\mathrm{RG}(\Gamma, \Gamma_n) = \lim_{n\to+\infty} r(\Gamma, \Gamma_n)
\]
exists, and is called the rank gradient of \( (\Gamma, (\Gamma_n)) \).

If \( (\Gamma_n), (\Delta_n) \) are two residual chains in the same group \( \Gamma \) (chains with \( \Gamma_n, \Delta_n \) normal in \( \Gamma \) and \( \bigcup_n \Gamma_n = \{ 1 \} = \bigcup_n \Delta_n \)), then are \( \mathrm{RG}(\Gamma, (\Gamma_n) \) and \( \mathrm{RG}(\Gamma, (\Delta_n)) \) equal?

One of the motivations for this is the following problem in 3–dimensional topology. Let \( M \) be a closed hyperbolic 3–manifold with Heegard genus \( g(M) \). Then \( d(\pi_1(M)) \le g(M) \). The « rank vs. gradient » problem was to determine whether equality always holds; Tao Li proved that for any \( C > 0 \) there exists an hyperbolic 3–manifold with \( g(m) – d(\pi_1(M)) \ge C \), answering this in the negative. On the other hand the following problem is still open:

Is the quotient \( d(\pi_1(M)) / g(M) \) bounded on the set of all closed hyperbolic 3–manifolds?

Combinatorial cost

Let \( \Gamma \) act via \( \phi \) on a set \( X \) preserving a probability measure \( \mu \). The associated measured groupoid \( \mathcal G \) is defined as follows: it is the set \(\Gamma \times X \) with the composition law \( (g, y) \cdot (h, x) = (gh, x) \) if \( \phi(h)x = y \). Let \( \tilde \mu \) be the product measure on \( \Gamma \times X \) (where \( \Gamma \) is endowed with the counting measure). Then the cost of the action is defined by:
\[
\mathrm{Cost}(\phi) = \inf(\tilde \mu(B): \langle B \rangle = \mathcal G).
\]
If \( \Gamma_n \) is any chain of finite-index subgroups then there is a natural action on the space \( \underset{\leftarrow}{\lim}(\Gamma/\Gamma_n) \) with the probability measure induced from the uniform measures on the finite sets \( \Gamma / \Gamma_n \) (this can be seen as the boundary of the rooted tree induced by the containment relation among cosets of the \( \Gamma_n \)).

Theorem (Abért–Nikolov): \( \mathrm{RG}(\Gamma, (\Gamma_n)) = \mathrm{Cost}( \underset{\leftarrow}{\lim}(\Gamma/\Gamma_n)) – 1 \).

This follows from the easily seen fact that the cost of the action on \( \Gamma/\Gamma_n \) equals \( r(\Gamma, \Gamma_n) + 1\) and « continuity » of the cost, which is the main step in the proof.

In case \( (\Gamma_n) \) is a residual chain the action is essentially free. For those actions Gaboriau asked the following question:

Fixed price conjecture: Is it true that the cost of an essentially free action depends only on the group acting?

Note that since it is possible to construct residual chains in a hyperbolic 3–manifold group which have rank sublinear in the index, a positive answer to this implies a negative answer to the question on rank vs. genus above.

Distortion functions

If \( \mathcal G \) is a groupoid on a set \( X \) generated by a subset \( B \) then we can form the Cayley graph of \( \mathcal G, B \). If we have two generating sets \( B, B’ \) then the bilipschitz constant of the identity map \( X \to X \) between the two Cayley graphs is denoted by \( d_b(B, B’) \in [1, +\infty] \).

If \( \mathcal G \) is the groupoid induced by the action of a group \( \Gamma \) on a probability space \( (X, \mu) \) then an obvious generating set for \( \mathcal G \) is \( S \times X \). Let \( c \) be the cost of the action and define:
\[
f(\varepsilon) = \inf( d_b(X\times S, B): \langle B \rangle = \mathcal G, \tilde \mu(B) \le c + \varepsilon)
\]
the distortion function of the action. Informally the decay of this as \( \varepsilon \to 0 \) measures how complicated a near-optimal generating set must be.

Theorem (Abért–Gelander–Nikolov): Let \( \Gamma_0 = \Gamma \supset \Gamma_1 \supset \cdots \) be a chain of subgroups. Let \( f \) be the distortion function of the action of \( \Gamma \) on \( \underset{\leftarrow}{\lim}(\Gamma / \Gamma_n) \). If \( f \) decays subexponentially at \( 0 \) (meaning that \( \lim_{\varepsilon \to 0} \log f(\varepsilon)/\varepsilon = +\infty \)) then
\[
\lim_{n \to +\infty} \frac{\log|H_1(\Gamma_n; {\mathbb Z})_{\mathrm{tors}}|} {|\Gamma / \Gamma_n|} = 0.
\]

A similar result can also be proved for sequences of subgroups which are not necessarily chains. For this the notion of combinatorial cost of a sequence of finite-index subgroups is needed. This is defined for a sequence \( (G_n) \) of graphs with uniformly bounded degree; then ait can be applied to a sequence of subgroups \( \Gamma_n \subset \Gamma \) via their Schreier graphs. Define:
\[
e((G_n)) = \lim_{n\to +\infty} \frac{|E(G_n)|}{|V(G_n)|}.
\]
A rewiring of the sequence \( (G_n) \) is a sequence \( (H_n) \) such that \( V(H_n) = V(G_n) \) and the bilipschitz distance between \( G_n \) and \( H_n \) is uniformly bounded; this is denoted by \( (H_n) \sim (G_n) \). The combinatorial cost is then defined by:
\[
\mathrm{cc}((G_n)) = \inf_{(H_n) \sim (G_n)} e((H_n)).
\]

A fundamental example of rewiring is as follows. Let \( G_n \) be the \( n \times n \) square grid and let \( K \ge 1 \). Let \( H_n \) be obtained as follows:

• keep all vertical edges;
• in each even column of \( G_n \) delete every horizontal edge but those on the lines indexed by integers \( = 0 \pmod K \);
• on odd columns delete every horizontal edge but those indexed by integers \( = \lfloor K/2 \rfloor \pmod K \)

as illustrated by the following figure:

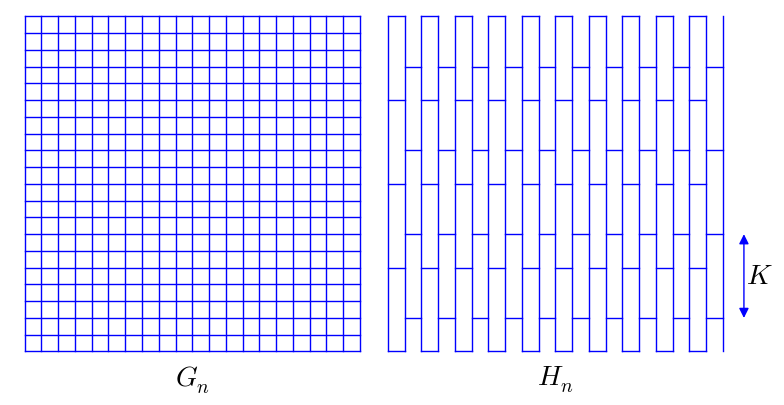
Then \( (H_n) \) is a rewiring of \( (G_n) \) (the bi-Lipscitz constants are bounded by \( K ) \) and it follows that \( \mathrm{cc}((G_n)) = 1 \).

Right-angled groups

A group \( \Gamma \) is called right-angled if there exists a finite generating set \( g_1, \ldots, g_d \) such that \( g_i g_{i+1} = g_{i+1}g_i \) and each \( g_i \) is of infinite order (to avoid the stupid case \( g_{2i+1} = 1 \)). There are many interesting examples:

• Many lattices in higher rank Lie groups are virtually right-angled;
• Right-angled Artin groups with connected graph are right-angles;
• On the other hand free groups are not right-angled;
• Most lattices in rank 1 Lie groups are not right-angled.

Theorem (Abért–Gelander–Nikolov): If \( \Gamma \) is right-angled, then for any residual chain \( \mathrm{RG}(\Gamma, (\Gamma_n)) = 0 \) and the growth of the torsion subgroup of \( H_1(\Gamma_n; {\mathbb Z}) \) is subexponential.

As a final remark note that there is no known example of a finitely presented, residually finite group \( \Gamma \) with a residual chain \( \Gamma_n \) satisfying
\[
\limsup_{n\to+\infty} \frac{\log|H_1(\Gamma_n; {\mathbb Z})_{\mathrm{tors}}|}{|\Gamma / \Gamma_n|} > 0
\]
although a conjecture of Bergeron–Venkatesh asserts that this should be the case for lattices in \( \mathrm{PSL}_2({\mathbb C}) \).