Cost of amenable groups

The aim of these notes is to provide an introduction to Gaboriau’s paper « Sur le coût des relations d’équivalence et des groupes » and to gather in one place various arguments, occuring in diverse sources, to give a characterisation of amenable groups through their actions on probability spaces.

Cost

Setting

Let $ X, \mathcal B, \mu $ be a measured space (often we’ll omit $ \mathcal B $ from the notation). Usually $ \mu $ will be a probability measure (i.e. $ \mu(X) = 1 $). Let $ E \subset X \times X $ be an equivalence relation on $ X $, we will use the abbreviation $ xEy $ for $ (x, y) \in E $. We will suppose that:

$ E $ is measurable, meaning that it is a measurable subset of $ X \times X $; equivalently, if $ A \in \mathcal B $ then also $ \{ x : \exists y \in A : xEy \} \in \mathcal B $.
All equivalence classes for $ E $ are countable.
$ \mu $ is $ E $-invariant, that is for any partially defined Borel isomorphism $ \phi : A \to B $ (where $ A, B \in \mathcal B $) such that $ \forall x \in A: xE\phi(x) $ we have $ \phi_*\mu|_A = \mu|_B $.

The basic example is when a finitely generated group $ \Gamma $ acts on a space $ X, \mu $ by Borel automorphisms preserving the measure $ \mu $(if in addition $ \mu $ is a probability measure we’ll say that this is a p.m.p.—for probability measure preserving—action), and $ E $ is the orbit relation: $ xEy \Leftrightarrow \exists \gamma \in \Gamma: y =\gamma \cdot x $.

The group of Borel automorphisms whose graph is contained in $ E $ (the full group of $ E $) is denoted by $ [E] $. The pseudo group of partially defined Borel automorphisms with graph contained in $ E $ is denoted by $ [[E]] $.

Graphings and cost of relations

A graphing of $ E $ is an undirected graph $ \mathcal G $ on $ X $ such that:

$ \mathcal G $ is contained in $ E $ : that is, if $ x, y $ are neighbours in $ \mathcal G $ then $ xEy $ (connected components of $ \mathcal G $ are contained in $ E $-classes);
$ \mathcal G $ generates $ E $: that is, if $ xEy $ then $ x, y $ are in the same connected component of $ \mathcal G $.
$ \mathcal G $ is measurable in the sense that the subset of $ X \times X $ given by those $ (x, y) $ which are neighbours in $ \mathcal G $ is measurable.

Equivalently, a graphing is defined by a collection $ \Phi = (\phi_i : A_i \to B_i)_{i \in I} $ of partially defined Borel automorphisms, such that:
\[
xEy \Leftrightarrow \exists i_1, \ldots, i_r \in I : y = \phi_{i_r} \circ \cdots \circ \phi_{i_1} x.
\]
The cost of a graphing $ \mathcal G $ (with respect to the measure $ \mu$) is half the average vertex degree:
\[
\mathrm{cost}(\mathcal G, \mu) = \frac 1 2 \int_X d_{\mathcal G}(x) d\mu(x)
\]
(where $ d_{\mathcal G}(x) $ is the number of neighbours of $ x $ in $ \mathcal G $). If the graphing is defined by $ \Phi $ as above then the cost is equal to:
\[
\mathrm{cost}(\Phi, \mu) = \sum_{i \in I} \mu(A_i).
\]
The cost of a measured equivalence relation is the smallest possible cost for a graphing:
\[
\mathrm{cost}(E, \mu) = \inf_{\mathcal G} \mathrm{cost}(\mathcal G, \mu).
\]

Cost of groups and fixed price

The cost of a discrete group $ \Gamma $, denoted by $ \mathrm{cost}(\Gamma) $, is the infimum over all of its essentially free, p.m.p. actions of their cost. A group is said to have fixed price if the cost of any action is equal to the cost of the group. There are no known exemples of a group which does not have fixed price.

Computing cost

Basic properties

Let $ X, \mu $ a probability space and $ E $ a measured equivalence relation on $ X $ preserving $ \mu $, with infinite countable classes. Then we have the following facts due to Levitt:

$ \mathrm{cost}(E, \mu) \ge 1 $.
If there exists a graphing $ \mathcal G $ such that $ \mathrm{cost}(E, \mu) = \mathrm{cost}(\mathcal G, \mu) $ then almost all components of $ \mathcal G $ are trees; it is then referred to as a treeing.
If $ B \subset X $ is a positive subset (measurable with positive measure) and $ E $ has finite cost then
\[
\mathrm{cost}(E|_B, \mu|_B/ \mu(B)) – 1 = \mu(B)^{-1} (\mathrm{cost}(E, \mu) – 1)
\]
Moreover $ E|_B $ admits a treeing if and only if $ E $ does.

We give two proofs of 1.: the one by Levitt, and one by Gaboriau which deduces it immediately from 3 (they are essentially the same).

Levitt’s proof goes as follows: for a partial graphing $ \Phi $ of $ E $ (a Borel graph contained in $E$ but which does not necessarily generate it) let
\[
e(\Phi) = \int_X \frac 1 {|\langle \Phi \rangle x|} d\mu(x).
\]
This is 0 if $ \Phi $ is a graphing (all orbits are infinite), and in general it is equal to the infimum over the measures of all Borel sets meeting every orbit of $ \langle \Phi \rangle $. The claim is then that for all partial graphings we have
\[
(\ast) \qquad e(\Phi) + \mathrm{cost}(\Phi) \ge 1.
\]
This is proven by induction: for the empty graphing we have $ e = 1, \mathrm{cost} = 0 $. Now suppose that $ \Phi $ satisfies $ (\ast) $ and $ \psi = \Phi \cup \{\psi : U \to V \} $. Let $ A $ be any Borel subset meeting every orbit of $ \langle \Psi \rangle $: we want to find a subset $ B $ such that $ A \cup B $ meets every orbit of $ \langle \Phi \rangle $ and $ \mu(B) \le \mu(A) + \mu(U) $ (then we get $ \mathrm{cost}(\Phi) + \mu(U) \ge \mathrm{cost}(\Psi) $ and if, fixing an aritrarily small $ \varepsilon > 0 $ we choose $ B $ such that $ \mu(B) \le e(\Psi) + \varepsilon $ also
\[
e(\Phi) \le \mu(A) \le \mu(B) + \mu(U) \le e(\Psi) + \varepsilon + \mathrm{cost}(\Psi) – \mathrm{cost} \Phi
\]
which proves that $ \mathrm{cost}(\Psi) + e(\Psi) \ge \mathrm{cost}(\Phi) + e(\Phi) $).

For $ x \in X $ there exists $ a \in A $ and $ \phi_{i_k} \in \Phi, m_k \in \mathbb Z $, $ k = 1, \ldots, n $ such that $ x = \prod_{k=1}^n \phi_{i_k} \psi^{m_k} $. Let $ s(x) = \inf \sum_k |m_k| $ and define:
\[
B_1 = \{ x \in U : s(\psi x) < s(x) \}, \quad B_2 = \{ x \in V : s(\psi^{-1}x) < s(x) \}.
\]
Then $ \psi^{-1}B_2 \subset U $ and $ B_1 \cap \psi^{-1} B_2 = \emptyset $ so that $ \mu(B_1) + \mu(B_2) \le \mu(U) $. In addition it is clear that $ X = \langle \Phi \rangle B $, which finishes our proof in case $ \Phi $ is a finite graphing. If $ \Phi = ( \phi_i, i \in \mathbb N ), \Phi_n = (\phi_k, 1\le k \le n) $ then we can conclude bu using $ \mathrm{cost}(\Phi_n) + e(\Phi_n) \ge 1 $ and $ \mathrm{cost}(\Phi) = \lim\mathrm{cost}(\Phi_n) $ and $ \lim e(\Phi_n) = 0 $.

Gaboriau’s proof runs as follows: if $ \Phi $ is a graphing then we know that $ e(\Phi) = 0 $ and thus for every $ \varepsilon $ there is a subset $ X_\varepsilon $ which meets every orbit and has $ \mu(X_\varepsilon) = \varepsilon $. By 3. we have
\[
\mathrm{cost}(\Phi) – 1 = \mu(X_\varepsilon)(\mathrm{cost}(\Phi|_{X_\varepsilon}) – 1) \ge -\mu(X_\varepsilon) = -\varepsilon
\]
since cost is positive, and by taking $ \varepsilon \to 0 $ we conclude that $ \mathrm{cost}(\Phi) – 1 \ge 0 $.

The proof of 2. is as follows. Suppose that $ \Phi $ is a graphing of $ E $ which is not a treeing. Then there exists $ i_k, \varepsilon_k \in \{ \pm 1\}, k=1, \ldots, n $ and a nonzero set $ A $ such that $ \prod_{i=1}^n \phi_{i_k} x = x $ for all $ x \in A $. We may in addition assume that $ \prod_{i=1}^p \phi_{i_k}^{\varepsilon_k} x \not \in A $ for all $ p \le n-1 $ and that $ \varepsilon_k = 1 $. Then the graphing which has $ \phi_{i_k} : A_{i_k} \to B_{i_k} $ by $ \phi_{i_k} : A_{i_k}\setminus A \to B_{i_k}\setminus \phi_{i_k}A $ has the same orbits as $ \Phi $ and cost equal to $ \mathrm{cost}(\Phi) – \mu(A) $, so that $ \mathrm{cost}(\Phi) > \mathrm{cost}(E) $.

When is cost realised by a single graphing?

The main theorem in Gaboriau’s paper is the converse of 2. An immediate corollary is that any essentially free action of a free group on $ r $ generators has cost $ r $, hence the group has fixed price $ r $.

Theorem : If $ \mathcal G $ is a treeing of $ E $ then $ \mathrm{cost}(E, \mu) = \mathrm{cost}(\mathcal G, \mu) $.

A more precise special case is the following, essentially due to Ornstein–Weiss in the hard direction and appearing in Levitt’s paper.

Theorem : Let $ E $ be the relation induced by an essentially free p.m.p. discrete group action. Then there exists a graphing $ \mathcal G $ with $ \mathrm{cost}(E) = \mathrm{cost}(\Phi) = 1 $ if and only if $ \Gamma $ is amenable.

Modulo an easy argument (to go from « heving a graphing with cost 1 » to « being generated by a single automorphism ») this means that:

If the orbits of $ \Gamma $ on $ X $ are equal to the orbits of a single Borel automorphism $ T : X \to X $ then $ \Gamma $ is amenable;
Conversely, if $ \Gamma $ is amenable there exists a $ T $ whose orbits are exactly that of $ \Gamma $.

The proof of the reciprocal direction 1 goes as follows: the orbit equivalence between $ \Gamma $ and $ \langle T \rangle \cong \mathbb Z$ gives a measure equivalence between these two groups, i.e. a measure space $ \widehat X, \widehat \mu $ with an action of $ \Gamma \times \mathbb Z $ such that both factors admit a finite-volume fundamental set. (This can be obtained as $ \widehat X = X \times \mathbb Z $ with $ \mathbb Z $ acting on the right by translations in the $ \mathbb Z $ factor and $ \Gamma $ acting by $ \gamma\cdot(x, n) = (\gamma x, n+m ) $ where $ \gamma x = T^m x $).

Now this measure equivalence gives a map $ \pi \mapsto \tilde \pi $ from unitary representations of $ \mathbb Z $ to those of $ \Gamma $. If $ \pi $ is defined on a Hilbert space $ \mathcal H $ then the representation $ \tilde \pi $ is defined on the space:
\[
\tilde{\mathcal H} := \left\{ f: \widehat X \to \mathcal H: \forall m \in \mathbb Z, x \in \widehat X : f(x\cdot m) = \pi(m)f(x) \right\}
\]
on which it acts by $ \tilde \pi(\gamma)f(x) = f(\gamma^{-1} \cdot x) $. Then we have the following facts:

If $ \pi $ is the left-regular representation on $ L^2(\Lambda) $ then $ \tilde \pi $ is equivalent to the representation on $ L^2(\widehat X) $ (which is equivalent to the Hilbert sum $ w_n \in \overline \bigoplus_{\mathbb Z} L^2(\Gamma) $ of countably many copies of the left-regular representation on $ L^2(\Gamma) $).
If $ \pi $ has almost-invariant vectors then $ \tilde \pi $ also does.

Thus if $ \Lambda $ is amenable, we get a sequence of quasi-$ \Gamma $-invariant vectors $ w_n \in \overline \bigoplus_{\mathbb Z} L^2(\Gamma) $. Projecting them onto the factors gives a sequence of quasi-invariant vectors in $ L^2(\Gamma) $, hence it is amenable.

Proof of (a) and (b): For (a) we have the map from $ \tilde H $ to $ L^2(\widehat X) $ given by $ f \mapsto \langle f, \delta_{1_\Lambda} \rangle_{L^2(\Lambda)} $ which is easily checked to be an isometry and $ \Gamma $-equivariant. For (b), we choose a mesurable fundamental domain $ U \subset \widehat X $ for $ \Lambda $. Given a sequence $ v_n \in \mathcal H, \| v_n \|_{\mathcal H} = 1 $ of quasi -invariant vectors (meaning that $ \langle \pi(g)v_n, v_n \rangle_{\mathcal H} \to 1 $ for every $ g \in \Lambda $) we define $ f_n \in \tilde H $ by $ f_n(x) = v_n $ for $ x \in U $. Then $ f_n $ is a sequence of quasi-invariant vectors in $ L^2(\Gamma) $.

Rokhlin lemma and cost of amenable groups

Now we want to prove that if $ \Gamma $ is amenable then the orbit relation of every p.m.p. $ \Gamma $-action is generated by a single Borel automorphism. For this we will use the following characterisation: an equivalence relation is said to be hyperfinite if there exists a nested sequence of finite, measurable subrelations $ F_1 \subset \cdots \subset F_n \subset E $ such that $ E = \bigcup_n F_n $.

Lemma : A measurable equivalence relation is hyperfinite if and only if it is induced by a single Borel automorphism.

The construction of an automorphism from a sequence of nested finite relations is illustarted by the following pictures.

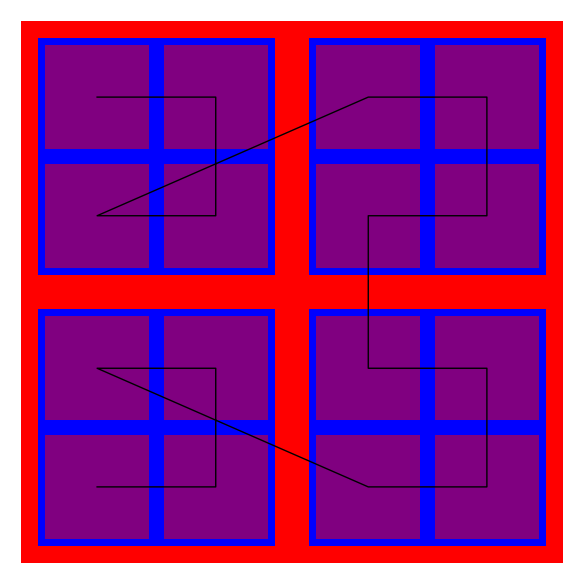
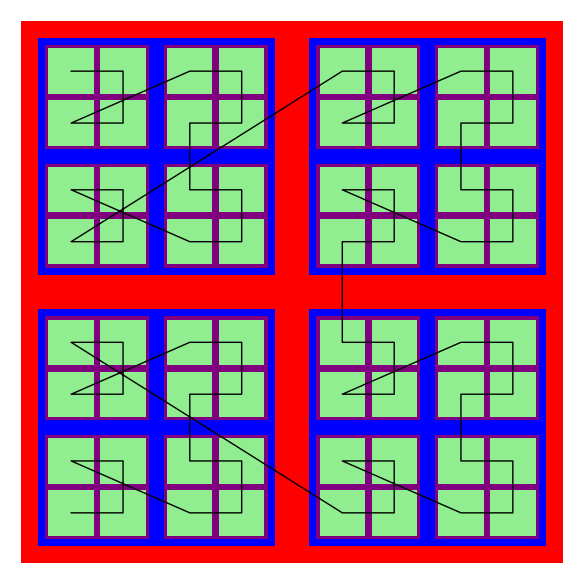
Thus we want to prove that an action of an amenable group gives rise to an hyperfinite equivalence relation. The result that will enable us to do so is the following theorem of Ornstein and Weiss, often called « Rokhlin’s lemma » (Rokhlin proved the case $ \Gamma = \mathbb Z $). Say that a finite subset $ T \subset \Gamma $ is a tile if there exists $ C \subset \Gamma $ such that $ \Gamma = CT $ and $ cT \cap c’T = \emptyset $ if $ c \not= c’ \in C $?

Theorem : Suppose that $ \Gamma $ is an amenable group and that $ T \subset \Gamma $ is a tile. Let $ \Gamma $ acting on (X, \mu) \) be an essentially free p.m.p. action. Then for any $ \varepsilon > 0 $ there exists a measurable subset $ A \subset X $ such that $ \mu(T \cdot A) \ge 1 – \varepsilon $ and for almost all $ a \in A $ we have $ (T\cdot) a \cap (T\cdot b) = \emptyset $ for all $ b \in A\setminus\{a\} $.

To deduce hyperfiniteness from this result suppose that there exists a sequence $ T_1, \ldots, T_n, \ldots $ of tiles such that $ T_n $ is $ (T_{n-1} \cup T_{n-1}^{-1}, 1/n) $-invariant. Let $ T_n’ = T_n \setminus (T_n \Delta T_{n-1}T_n) $ so that $ |T_n’|/|T_n| \ge 1 – 1/n $.

Rokhlin’s lemma gives us subsets $ A_n \subset X $ such that $ \mu(T_nA_n) \ge 1-1/n $ and the $ T_na, a \in A_n $ are paiwise disjoint. Let $ F_n $ be the finite relation which is defined by
\[
xF_n y \Leftrightarrow \exists a \in A: x, y \in T_na
\]
on $ T_nA $ and which is the identity on $ X \setminus T_nA $. Clearly $ E = \bigcup_n F_n $ (because $ \Gamma = \bigcup_n T_n $); the problem with $ F_n $ is that we don’t have $ F_{n-1} \subset F_n $.

Let $ F_n’$ be defined as follows: a class $ [F_n]x $ contains exactly one « large » class for $ F_n’ $ consisting of all $ yF_nx $ such that $ [F_n’]y \subset [F_n]x $, and for all other points we take their $ F_{n-1}’ $-class. Clearly $ F_{n-1}’ \subset F_n’ $, and also $ T_n’a \subset [F_n’]a $ for all $ a \in A_n $. It follows from the latter that $ E = \bigcup_n F_n’ $.

Note that it is not known whether all amenable groups admit such a sequence of tiles; however, this is the case for all elementary amenable groups (Ornstein–Weiss) and for all residually finite amenable groups (Weiss). In general one has to use almost-tilings, for which the Rokhlin lemma also holds.

Proof of the Rokhlin lemma

The first step is to establish the following lemma.

For any $ \varepsilon > 0 $ and $ n \ge 1 $ there is a finite subset $ H \subset \Gamma $ which is $ T \cup T^{-1}, \varepsilon^2 $-invariant an a collection of measurable subsets $ U_1, \ldots, U_m \subset X $ such that :

for all $ i = 1, \ldots, n $ and $ u \not= u’ \in U_i $ the sets $ Hu, Hu’ $ are disjoint;

$ \mu\left( \bigcup_i U_i \right) \ge 1 – \varepsilon $;

$ \sum_i \mu(U_i) \le \varepsilon^{-1} $.

To prove this Ornstein and Weiss use the following two statements:

There is a cover of $ X $ by pairwise disjoint sets $ U_i, i \in \mathbb N $ satisfying 1) ;
Given $ \varepsilon > 0 $ and a cover $ X = \bigcup_{j \ge 1} V_j $ such that every $ x \in X $ belongs to exactly $ N $ of the $ V_j $ there exists a finite subsequence $ V_{j_i}, i=1, \ldots, N $ which satisfies 2) and 3).

The point a) is easily proven once it is known that every subset of positive measure in $ X $ contains a set satisfying 1) (choose a first set $ U_1 $ with positive measure, and then do the same in $ X \setminus U_1 $,…) which is more or less obvious.

Point b) is a general fact in combinatorics, proven by Ornstein–Weiss using the following lemma : let $ X = \bigcup_i V_i $ be a cover by measurable such that every point belongs to exactly N of the $ V_i $s. Then for any $ V \subset X $ there exists $ V_i $ such that :
\[
(\ast\ast) \qquad \frac{\mu(V_i \cap V)}{\mu(V_i)} \le \mu(V).
\]
Now suppose that the $ U_i $ are ordered by measure (so that $ \mu(U_{i+1}) \le \mu(U_i) $) and use $ (\ast\ast) $ to construct a maximal sequence $ i_1 = 1, i_2, \ldots $ such that for all $ k \le n-1 $ ($ n \in \mathbb N \cup\{\infty\} $ the length of the sequence) $ \mu(\bigcup_{1\le l \le k} U_{i_l}) < 1 – \varepsilon $, $ \mu(U_{i_k} \cap \bigcup_{1\le l \le k-1} U_{i_l}) \le \mu(U_{i_k})\mu(\bigcup_{1 \le l \le k-1} U_{i_l}) $ and $ i_k $ is the smallest index with these properties. If $ n < +\infty $ this finishes the proof. Otherwise, if we had $ \mu(\bigcup_{l \ge 1} U_{i_l}) < 1 – \varepsilon $, by $ (\ast\ast) $ there would be an index $ j \in \mathbb N $ such that $ \mu(U_j \cap \bigcup_{l\ge 1} U_{i_l}) \le \mu(U_j)\mu(\bigcup_{1 \le l} U_{i_l}) $ and this contardicts the choice of the $ U_{i_k} $.

In addition, the fact that $ \mu(U_{i_k} \cap \bigcup_{1\le l \le k-1} U_{i_l}) \le (1 – \varepsilon) \mu(U_{i_k}) $ easily implies that $ \sum_{l \ge 1} \mu(U_{i_l}) \le \varepsilon^{-1} $.

For the second step let $ C \subset \Gamma $ such that $ | TC \Delta H | \le \varepsilon^2 | H | $ which exists because $ T $ tiles and H is $ TT^{-1}, \varepsilon^2 $-invariant. Let $ W_i = \bigcup_{j=1}^i HU_j $ and construct inductively sets $ W_i’ $ such that $ W_i’ $ contains all $ Tcu, u \in U_i, c \in C $ such that $ Tcu \cap U_{i+1} = \emptyset $. We get
\[
\mu(W_i \setminus W_i’) \le \varepsilon^2 \sum_{j=1}^i \mu(U_j)
\]
so that in the end $ \mu(W_m’) \ge 1 – \varepsilon – \varepsilon^2 \sum_{j=1}^i \mu(U_j) \ge 1 – 2\varepsilon $. The other conclusion of the Rokhlin lemma clearly holds for the set
\[
A = \bigcup_{i=1}^m \{ cu : u \in U_i, c \in C : (Tcu) \subset X \setminus \bigcup_{j \ge i+1} HU_j
\]
which satisfies $ TA = W_m’ $, and this finishes the proof.

Références

Gilbert Levitt, On the cost of generating an equivalence relation, Ergodic Theory and Dynamical systems.
Damien Gaboriau, Coût des relations d’équivalence et des groupes, Inventiones Mathematicae.
Donald Ornstein, Benjamin Weiss, Entropy and isomorphism theorems for actions of amenable groups, Journal d’analyse mathématique.
Alex Furman, A survey of measured group theory, in Geometry, Rigidity, and Group Actions, U. Chicago press.

Notes

Un site utilisant Blog IMT